数组

数组概述

数组概述

• 什么是数组？
1. 在 Java 中，数组是一种用于存储多个相同数据类型元素的容器。
2. 例如一个存储整数的数组：int[] nums = {100, 200, 300};
3. 例如一个存储字符串的数组：String[] names = {“jack”,“lucy”,“lisi”};
4. 数组是一种引用数据类型，隐式继承 Object。因此数组也可以调用 Object 类中的方法。
5. 数组对象存储在堆内存中。
• 数组的分类？
1. 根据维数进行分类：一维数组，二维数组，三维数组，多维数组。
2. 根据数组中存储的元素类型分类：基本类型数组，引用类型数组。
3. 根据数组初始化方式不同分类：静态数组，动态数组。
• Java数组存储元素的特点？
1. 数组长度一旦确定不可变。
2. 数组中元素数据类型一致，每个元素占用空间大小相同。
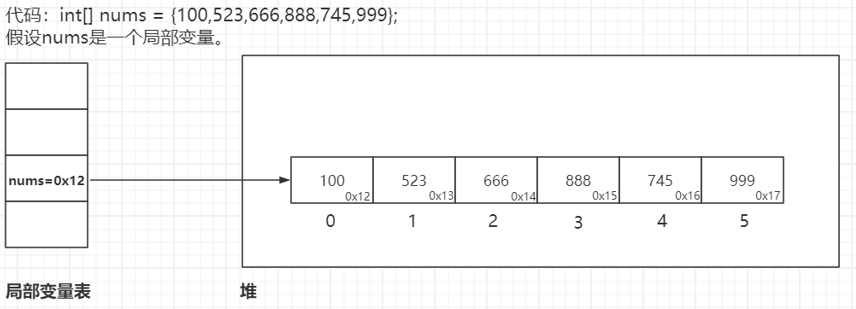
3. 数组中每个元素在空间存储上，内存地址是连续的。
4. 每个元素有索引，首元素索引 0，以 1 递增。
5. 以首元素的内存地址作为数组对象在堆内存中的地址。
6. 所有数组对象都有 length 属性用来获取数组元素个数。末尾元素下标：length-1

• 数组优点？
1. 根据下标查询某个元素的效率极高。数组中有 100 个元素和有 100 万个元素，查询效率相同。时间复杂度 O(1)。也就是说在数组中根据下标查询某个元素时，不管数组的长短，耗费时间是固定不变的。
2. 原因：知道首元素内存地址，元素在空间存储上内存地址又是连续的，每个元素占用空间大小相同，只要知道下标，就可以通过数学表达式计算出来要查找元素的内存地址。直接通过内存地址定位元素。
• 数组缺点？
1. 随机增删元素的效率较低。因为随机增删元素时，为了保证数组中元素的内存地址连续，就需要涉及到后续元素的位移问题。时间复杂度 O(n)。O(n)表示的是线性阶，随着问题规模 n 的不断增大，时间复杂度不断增大，算法的执行效率越低。（不过需要注意的是：对数组末尾元素的增删效率是不受影响的。）
2. 无法存储大量数据，因为很难在内存上找到非常大的一块连续的内存。

一维数组

一维数组

• 一维数组是线性结构。二维数组，三维数组，多维数组是非线性结构。
• 如何静态初始化一维数组？
1. 第一种：int[] arr = {55,67,22}; 或者 int arr[] = {55,67,22};
2. 第二种：int[] arr = new int[]{55,67,22};
• 如何访问数组中的元素？
1. 通过下标来访问。
2. 注意 ArrayIndexOutOfBoundsException 异常的发生。
• 如何遍历数组？
1. 普通 for 循环遍历
2. for-each 遍历（优点是代码简洁。缺点是没有下标。）
3. 练一练：获取 10 个学生成绩，然后把成绩保存在数组中，接着遍历数组获得学生成绩，最后计算总分和平均分。
• 如何动态初始化一维数组？
1. int[] arr = new int[4];
2. Object[] objs = new Object[5];
3. 数组动态初始化的时候，确定长度，并且数组中每个元素采用默认值。

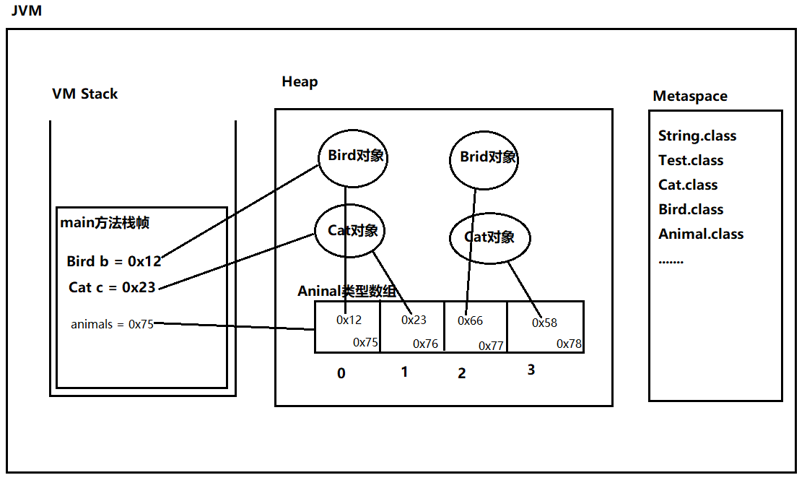
• 方法在调用时如何给方法传一个数组对象？
• 当一维数组中存储引用时的内存图？
• 如何获取数组中的最大值？
• 假设首元素是最大的，然后遍历数组中所有元素，只要有更大的，就将其作为最大值。
• 思考：找出最大值的下标怎么做？
• 如果知道值，如何通过值找它的下标？
• 如何将数组中的所有元素反转？
• 第一种方式：创建一个新的数组。
• 第二种方式：首位交换。
• 关于 main 方法的形参 args？
• 接收命令行参数
• 在 DOS 命令窗口中怎么传？在 IDEA 中怎么传？
• 关于方法的可变长度参数？
• 可变长参数只能出现在形参列表中的最后一个位置。
• 可变长参数可以当做数组来处理。

一维数组的扩容

• 数组长度一旦确定不可变。
• 那数组应该如何扩容？
• 只能创建一个更大的数组将原数组中的数据全部拷贝到新数组中
• 可以使用 System.arraycopy()方法完成数组的拷贝。
• 数组扩容会影响程序的执行效率，因此尽可能预测数据量，创建一个接近数量的数组，减少扩容次数。

二维数组

二维数组

• 二维数组是一个特殊的一维数组，特殊在：这个一维数组中每个元素是一个一维数组。
• 二维数组的静态初始化
• int[][] arr = new int[][]{ {},{},{} };
• int[][] arr = { {},{},{} };
• 二维数组的动态初始化(等长)
• int[][] arr = new int[3][4];
• 二维数组的动态初始化（不等长）
• int[][] arr = new int[3][];
• 二维数组中元素的访问
• 第一个元素：arr[0][0]
• 最后一个元素：arr[arr.length-1][arr[arr.length-1].length-1]
• 二维数组中元素的遍历

小项目

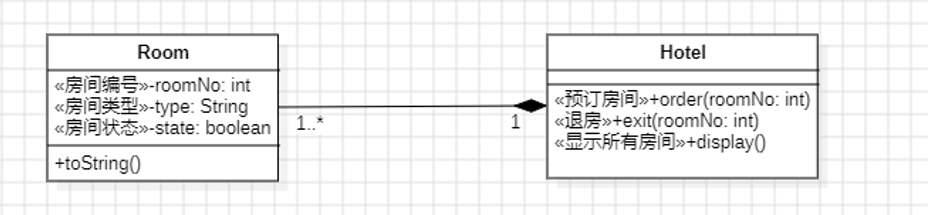
• 请使用二维数组实现酒店管理系统。功能如下：
1. 查看酒店所有房间的状态。
2. 预订房间。
3. 退房。
4. 退出系统。

练一练（实现一个学生管理系统）

1. 程序启动时，读取一个预设的学生数组，其中已经保存了学生信息（包括学生姓名、学号、出生日期、性别、联系方式等）。
2. 程序提供以下操作选项：

• 显示所有学生的信息
• 通过学号查找学生的信息
• 添加新的学生信息
• 修改学生信息
• 删除学生信息
• 退出程序

3. 添加新的学生信息时，要求输入学生所有信息，并自动添加到学生数组中，学号自动生成，不能与已有学生的学号重复。
4. 修改学生信息时，提示用户输入要修改的学生的学号，然后允许用户修改该学生的信息（包括姓名、出生日期、性别、联系方式等）。
5. 删除学生信息时，提示用户输入要删除的学生的学号，并将该学生从学生数组中删除。
6. 修改、添加和删除学生信息后，重新显示所有学生的信息。

IDEA 中的 Debug 调试

如何使用 IDEA 找 bug，解决问题

• 在可能出现问题的代码附近添加断点。一般是将断点添加在方法体的某一行代码上。
• 断点可以添加多个。点一次添加一个断点。再点一次断点则消失。
• 添加断点后，如果想让程序运行到断点处停下来，需要使用 Debug 模式运行程序。
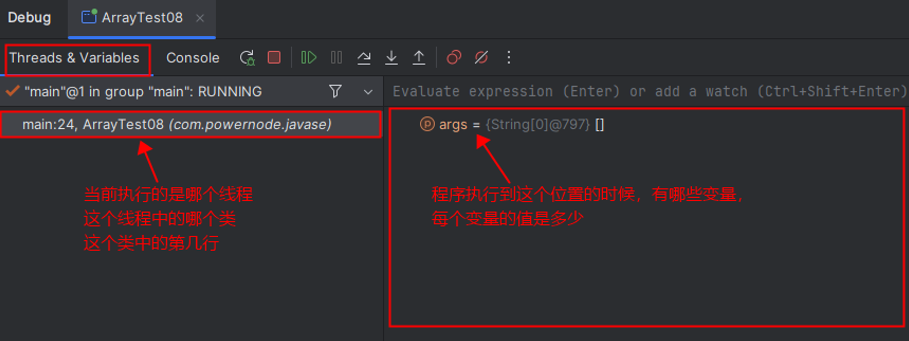
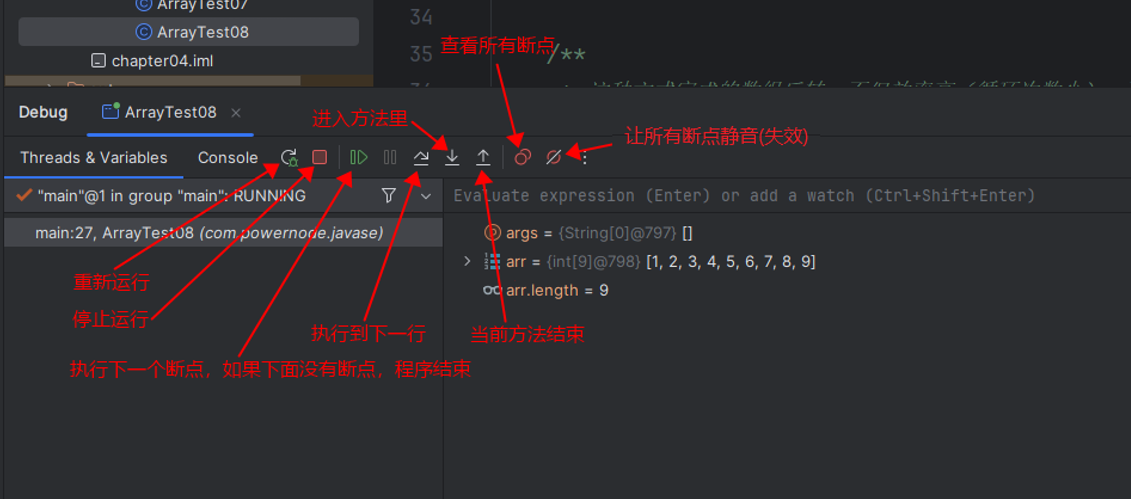
• Debug 窗口中的按钮
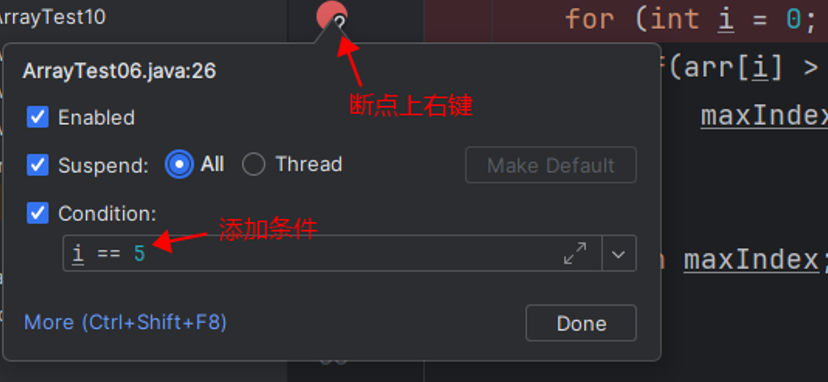
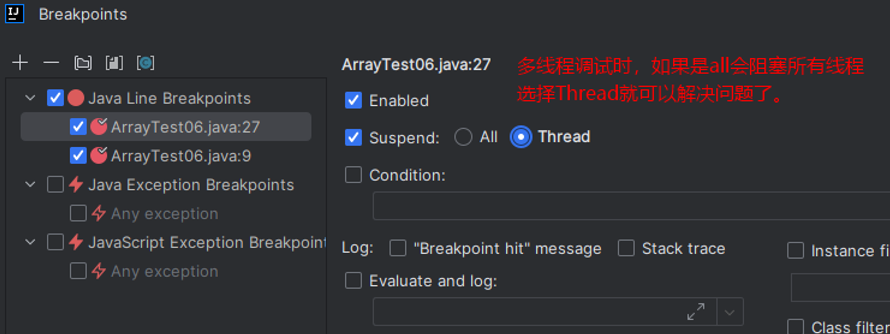
• 给断点添加条件
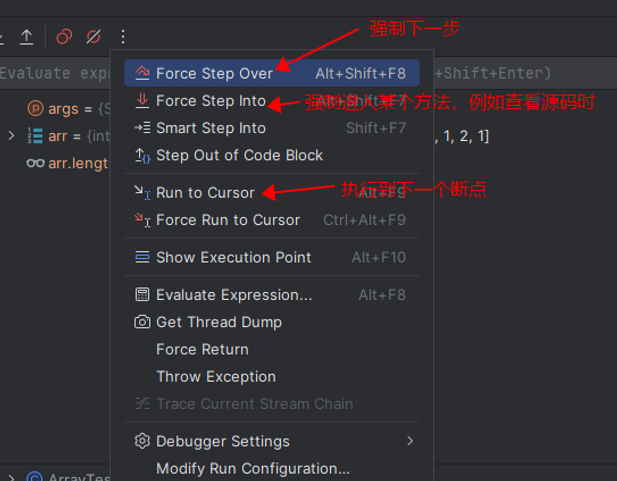
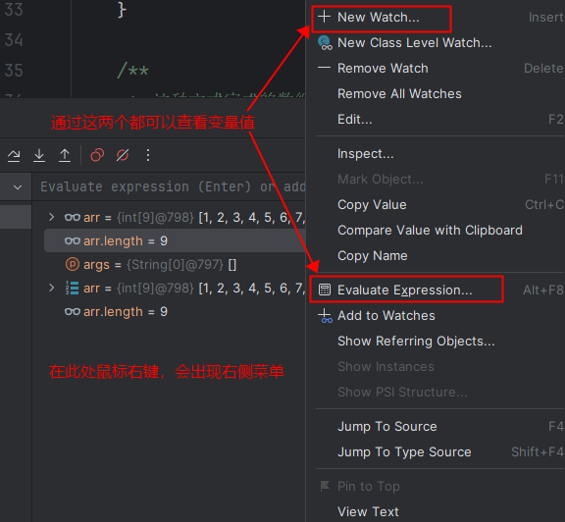
• Debug 窗口中的隐藏按钮

JUnit 单元测试

单元测试（JUnit5）

• 什么是单元测试，为什么要进行单元测试？

1.一个项目是巨大的，只有保证你写的每一块都是正确的，最后整个项目才能正常运行。这里所谓的每一块就是一个单元。

• 做单元测试需要引入 JUnit 框架，JUnit 框架在 JDK 中没有，需要额外引入，也就是引入 JUnit 框架的 class 文件（jar 包）
• 单元测试类（测试用例）怎么写？
1. 单元测试类名：XxxTest
• 单元测试方法怎么写？
1. 单元测试方法需要使用@Test 注解标注。
2. 单元测试方法返回值类型必须是 void
3. 单元测试方法形参个数为 0
4. 建议单元测试方法名：testXxx
• 什么是期望值，什么是实际值？
1. 期望值就是在程序执行之前，你觉得正确的输出结果应该是多少
2. 实际值就是程序在实际运行之后得到的结果
• 常见注解：
1. @BeforeAll @AfterAll 主要用于在测试开始之前/之后执行必要的代码。被标注的方法需要是静态的。
2. @BeforeEach @AfterEach 主要用于在每个测试方法执行前/后执行必要的代码。
• 单元测试中使用 Scanner 失效怎么办？
1. 选中导航栏的“Help”，然后选中“Edit Custom VM Options...”，接着在“IDEA64.exe.vmoptions”文件中添加内容“-Deditable.java.test.console=true”，最后在重启 IDEA 即可解决

数据结构与算法

数据结构概述

• 数据结构是指用来存储和组织数据的一种方式，就像在生活中我们用文件柜、书架、衣柜等来整理我们的物品一样，数据结构也可以帮助我们整理和管理程序中的数据。
• 数据结构分为：数据的逻辑结构、数据的物理结构
1. 逻辑结构是指数据元素之间的逻辑关系，它是从抽象的角度描述数据元素之间的关系，不涉及具体的存储方式或实现细节。逻辑结构主要关注问题的本质、特点和抽象模型，是数据结构的逻辑表示。
2. 物理结构是指数据结构在计算机内存中实际存储和组织的方式。它是从具体的角度描述数据结构的实现方式和存储结构，包括数据元素在内存中的存储分布和访问方式等。物理结构主要关注问题的具体实现和操作。
3. 因此，逻辑结构与物理结构的区别在于：逻辑结构是从抽象的角度描述数据元素之间的关系，物理结构是从具体的角度描述内存中数据元素的存储方式和组织形式。逻辑结构主要关注问题的本质和特点，物理结构主要关注问题的具体实现和操作。
• 逻辑结构的划分？
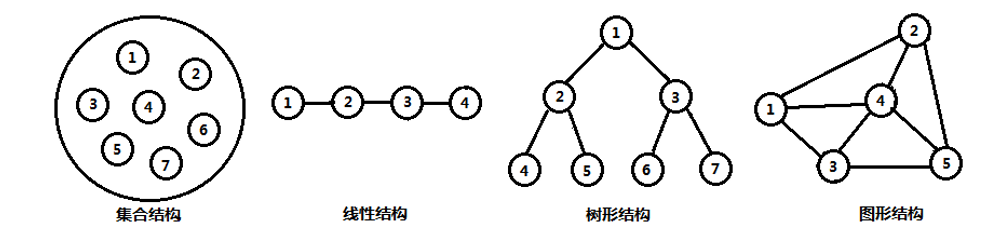
1. 集合结构：数据结构中的元素之间除了在“同属一个集合”的关系外，别无其它关系；
2. 线性结构：数据结构中的元素存在“一对一”的线性关系，例如冰糖葫芦；
3. 树形结构：数据结构中的元素存在“一对多”的层次关系，例如公司组织架构；
4. 图形结构或网状结构：数据结构中的元素存在“多对多”的任意关系，例如地图。
• 物理结构的划分？
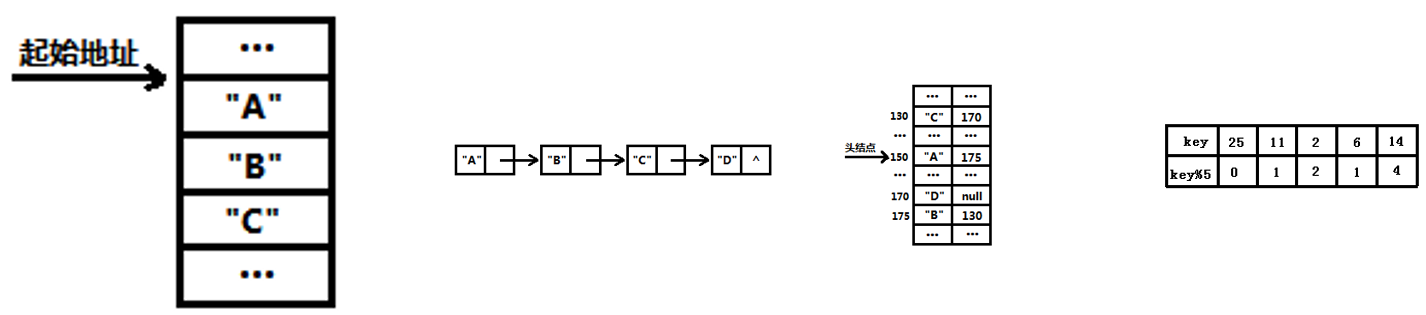
1. 顺序存储结构：用一组连续的存储空间单元来依次的存储数据元素，例如数组。
2. 链式存储结构：用一组任意的存储单元来存储元素，通过保存地址找到相关联的元素，元素之间的逻辑关系用引用来表示，例如链表。
3. 散列存储结构：根据节点 key 计算出该节点的存储地址。例如：java 集合中的 HashMap 采用了散列存储结构，添加、查询速度都很快。

算法概述

• 什么是算法？

算法就是解决问题的方法和步骤，可以让计算机完成特定任务，并提高计算机系统的效率和性能。就像烹饪食品需要遵循一定的步骤和配方一样，例如，做牛排需要选择牛排肉、煎炸的方式、烹饪的时间等，按照一定的步骤最终会有一个好的成品。一个良好的算法可以提高程序的执行效率。

• 怎么评价一个算法好不好？

如何计算 1+2+3+...+100 的结果？

1. 算法 1：通过循环，依次累加来实现。耗费时间
2. 算法 2：使用递归来实现。耗费内存
3. 算法 3：高斯算法。(1 + 100)*50。既节省时间，又节省空间。

同一问题可用不同的算法来解决，而一个算法的质量优劣将影响到算法乃至程序的效率。因此，我们学习算法目的在于选择合适算法和改进算法，一个算法的评价主要从时间复杂度和空间复杂度来考虑。

1. 时间复杂度：评估执行程序所需的时间，可以估算出程序对处理器的使用程度。
2. 空间复杂度：评估执行程序所需的存储空间，可以估算出程序对计算机内存的使用程度。

数据结构与算法的关系

• 程序的灵魂 = 数据结构 + 算法
• 数据结构可以提供算法的运行环境和基础，而算法又可以通过对数据结构的设计和操作，实现对数据的高效管理和处理。数据结构和算法是互相依存的，应该统一考虑，合理利用不同的数据结构和算法来解决实际问题，从而提高程序的执行效率。

时间复杂度

• 什么叫做时间复杂度？

我们用 T(n)来表示算法中基本操作（例如比较、赋值、运算等）的重复执行次数。n 是程序需要处理的数据量（专业术语叫做问题规模 n）。若有某个趋势函数 f(n)【f(n)代表了时间复杂度的趋势】，使得当 n 趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。记作 T(n)=O(f(n))，我们称 O(f(n))为时间复杂度。我们也把它叫做大 O 表示法。

• 时间复杂度计算步骤：
1. 计算基本操作的执行次数 T(n)

在做算法分析时，一般默认考虑最坏的情况。因为最坏的情况下，基本操作执行的次数是最多的。对算法效率的评估会更加准确。

2. 通过 T(n)得到 f(n)

求 T(n)的数量级 f(n)，只需要将 T(n)做两个操作：

（一）忽略常数项、低次幂项和最高次幂项的系数。

（二）例如，在 T(n)=4n2+2n+2 中，T(n)的数量级函数 f(n)=n2。

计算 T(n)的数量级 f(n)，我们只要保证 T(n)中的最高次幂正确即可，可以忽略所有常数项、低次幂项和最高次幂的系数。这样能够简化算法分析，将注意力集中在最重要的一点上：增长率。

3. 用大 O 表示时间复杂度

得到 f(n)的结果是 n2，所以时间复杂度是：O(n2)。

切记，时间频度不相同，时间复杂度有可能相同，如 T(n)=n2+3n+4 与 T(n)=4n2+2n+1 它们的时间频度不同，但时间复杂度相同，都为 O(n2)。

常见的时间复杂度

• 常数阶 O(1)

无论代码执行了多少行，只要没有循环等复杂结构，那这个代码的时间复杂度就都是 O(1)

int num1 = 3, num2 = 5;
int temp = num1;
num1 = num2;
num2 = temp;
System.out.println("num1:" + num1 + " num2:" + num2);

在上述代码中，没有循环等复杂结构，它消耗的时间并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用 O(1)来表示它的时间复杂度

• 对数阶 O(log2n)

O(log2n)指的就是：在循环中，每趟循环执行完毕后，循环变量都放大两倍。

int n = 1024;
for(int i = 1; i < n; i *= 2) {
    System.out.println("hello powernode");
}

推算过程：假设该循环的执行次数为 x 次（也就是 i 的取值为 2x），就满足了循环的结束条件，即满足了 2 x 等于 n，通过数学公式转换后，即得到了 x = log2n，也就是说最多循环 log2n 次以后，这个代码就结束了，因此这个代码的时间复杂度为：O(log2n) 。 同理，如果每趟循环执行完毕后，循环变量都放大 3 倍，那么时间复杂度就为：O(log3n) 。

• 线性阶 O(n)

int n = 100;
for(int i = 0; i < n; i++) {
  System.out.println("hello powernode");
}

在上述代码中，for 循环会执行 n 趟，因此它消耗的时间是随着 n 的变化而变化的，因此这类代码都可以用 O(n)来表示它的时间复杂度 。

• 线性对数阶 O(nlog2n)

int n = 100;
for(int i = 1; i <= n; i++) {
  for(int j = 1; j <= n; j *= 2) {
      System.out.println("hello powernode");
  }
}

线性对数阶 O(nlog2n) 其实非常容易理解，将时间复杂度为 O(log2n)的代码循环 n 遍的话，那么它的时间复杂度就是 n*O(log2n)，也就是了 O(nlog2n)。

• 平方阶 O(n2)

int n = 100;
for(int i = 1; i <= n; i++) {
  for(int j = 1; j <= n; j++) {
      System.out.println("hello powernode");
  }
}

外层 i 的循环执行一次，内层 j 的循环就要执行 n 次。因为外层执行 n 次，总的就需要执行 n*n 次，也就是需要执行 n2 次。因此这个代码时间复杂度为：O（n2）。

平方阶的另外一个例子：

int n = 100;
for(int i = 1; i <= n; i++) {
  for(int j = i; j <= n; j++) {
      System.out.println("hello powernode");
  }
}

当 i=1 的时候，内侧循环执行 n 次，当 i=2 的时候，内侧循环执行（n-1）次，......一直这样子下去就可以构造出一个等差数列：n+（n-1）+（n-2）+......+2+1≈(n2)/2。根据大 O 表示法，去掉最高次幂的系数，就可以得到时间复杂度为：O（n2）。

同理，立方阶 O(n3)，参考上面的 O(n2)去理解，也就是需要用到 3 层循环

• 指数阶 O(2n)

当 n 为 10 的时候，需要执行 210 次

• 阶乘阶 O(n!)

当 n 为 10 的时候，需要执行 10 * 9 * 8 * ... * 2 * 1 次

常见的时间复杂度耗时比较

• 算法的时间复杂度是衡量一个算法好坏的重要指标。一般情况下，随着规模 n 的增大，T(n)的增长较慢的算法为最优算法
• 其中 x 轴代表 n 值，y 轴代表 T(n)值。T(n)值随着 n 的值的变化而变化，其中可以看出 O(n!)和 O(2n)随着 n 值的增大，它们的 T(n)值上升幅度非常大，而 O(logn)、O(n)、O(nlogn)、O(n2)随着 n 值的增大，T(n)值上升幅度相对较小。
• 常用的时间复杂度按照耗费的时间从小到大依次是：O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!)

数组的排序算法

冒泡排序

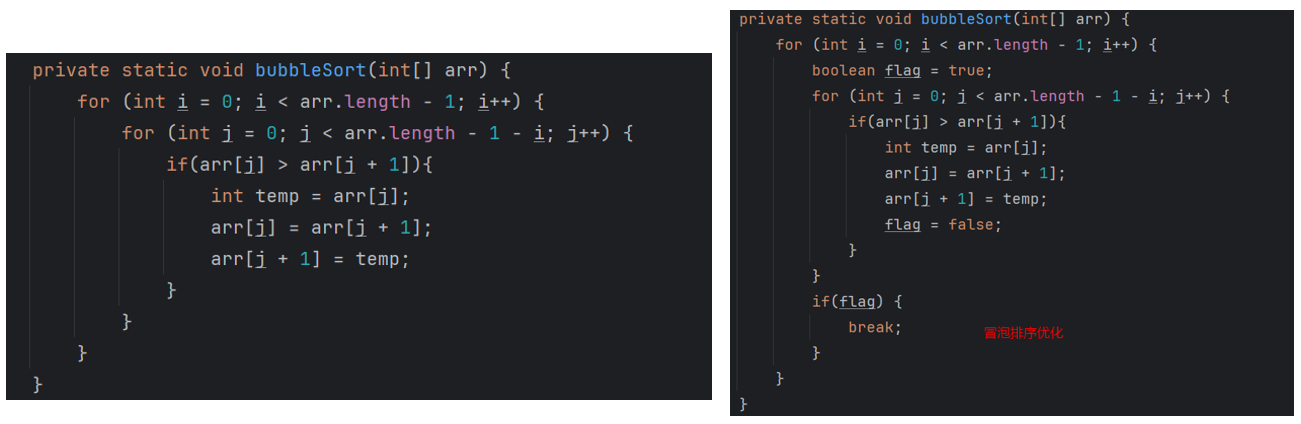
• 冒泡排序的核心思想？

相邻两个元素做比较大小，如果前一个元素大于后一个元素，则交换位置

• 升序排序代码如何实现？
• 冒泡排序算法优化？

因为冒泡排序存在提前排序成功的可能，因此我们需要对以上冒泡排序算法进行优化，此处的优化思路使用了“假设法”来实现

选择排序算法

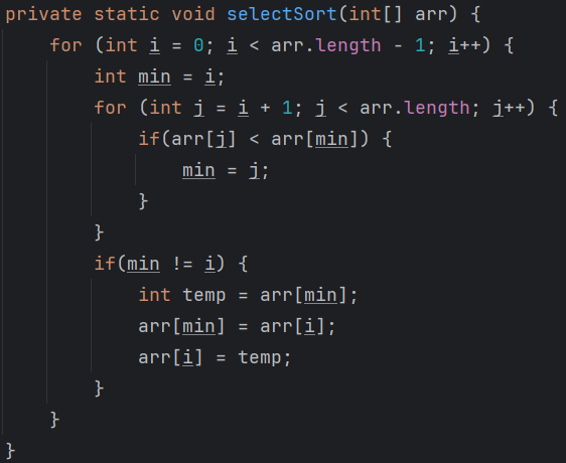
• 选择排序的核心思想？

在未排序的序列中，把未排序第一个元素和未排序的最小元素交换位置。

• 升序排序代码如何实现？

线性查找

• 线性查找是一种最简单粗暴的查找法了，采用逐一比对的方式进行对数组的遍历，如果发现了匹配值，返回数组下标即可。
• 线性查找，优点是查找数组无需有序；其缺点是查找的次数多，效率低下。

二分法查找

• 二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；缺点是要求待查数组必须排序，且执行插入和删除操作困难。因此，折半查找方法适用于不经常变动而查找频繁的数组。
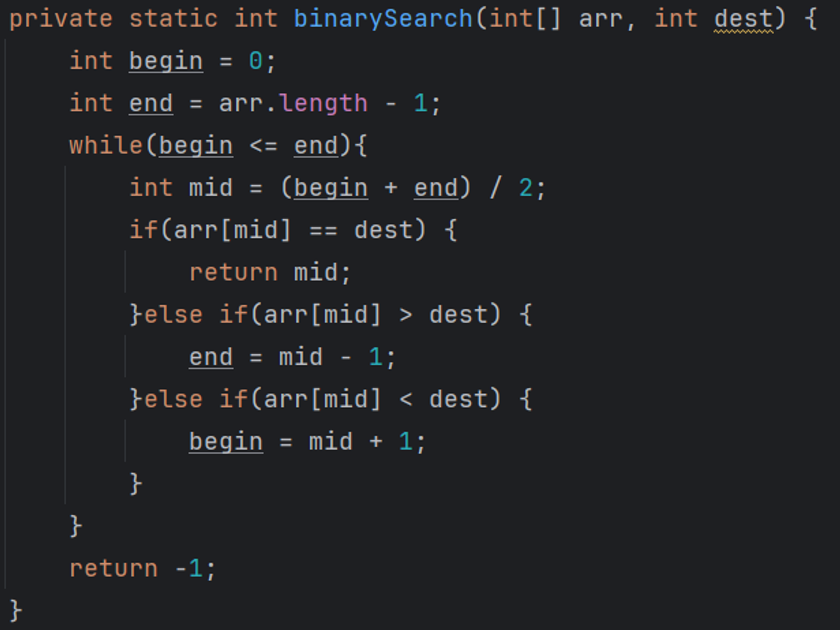
• 查找思路：

假设查找的数组为升序排序，则首先定义两个变量，分别用于保存查找元素（value）所在范围的最小索引值（min）和最大索引值（max）。

然后开启二分查找，每次查找前都定义一个 mid 变量，并设置该变量的初始值为：(max + min)/2。在查找的过程中，发生以下三种情况，则做对应的处理。

1. 如果 arr[mid]大于 value，则证明查找的元素在 mid 的左侧，那么更新 max 的值为：mid-1
2. 如果 arr[mid]小于 value，则证明查找的元素在 mid 的右侧，那么更新 min 的值为：mid+1
3. 如果 arr[mid]等于 value，则证明查找元素的索引值就是 mid，返回 mid 的值即可！

在以上的操作中，我们不停的更改 min 和 max 的值，如果发生 min 大于 max 的情况，则证明查找的元素不存在，那么返回-1（表示找不到）即可！

Arrays 工具类

Arrays 工具类

• Arrays.toString()方法：将数组转换成字符串
• Arrays.deepToString()方法：可以将二维数组转换成字符串
• Arrays.equals(int[] arr1, int[] arr2)方法：判断两个数组是否相等
• Arrays.equals(Object[] arr1, Object[] arr2)方法
• Arrays.deepEquals(Object[] arr1, Object[] arr2)方法：判断两个二维数组是否相等
• Arrays.sort(int[] arr)方法：基于快速排序算法，适合小型数据量排序。
• Arrays.sort(String[] arr)方法
• Arrays.parallelSort(int[] arr)方法：基于分治的归并排序算法，支持多核 CPU 排序，适合大数据量排序。
• int binarySearch(int[] arr, int elt)方法：二分法查找
• Arrays.fill(int[] arr, int data)方法：填充数组
• Arrays.fill(int[] a, int fromIndex, int toIndex, int val)方法
• int[] Arrays.copyOf(int[] original, int newLength)方法：数组拷贝
• int[] Arrays.copyOfRange(int[] original, int from, int to)
• Arrays.asList(T... data)方法：将一组数据转换成 List 集合。