队列结构（Queue）

认识队列

受限的线性结构：

我们已经学习了一种受限的线性结构：栈结构。
并且已经知道这种受限的数据结构对于解决某些特定问题，会有特别的效果。
下面，我们再来学习另外一个受限的数据结构：队列。

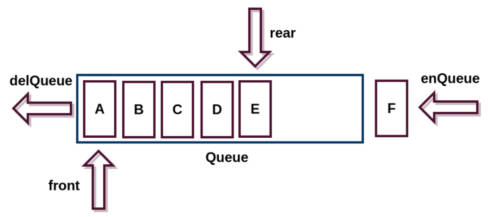
队列（Queue），它是一种受限的线性表，先进先出（FIFO First In First Out）

受限之处在于它只允许在队列的前端（front）进行删除操作：
而在队列的后端（rear）进行插入操作；

生活中的队列

生活中的队列结构

生活中类似队列的场景就非常多了
比如在电影院，商场，甚至是厕所排队
优先排队的人，优先处理。（买票、结账、WC）

开发中队列的应用

打印队列：

有五份文档需要打印，这些文档会按照次序放入到打印队列中。
打印机会依次从队列中取出文档，优先放入的文档，优先被取出，并且对该文档进行打印。
以此类推，直到队列中不再有新的文档。

编程队列：

在开发中，为了让任务可以并行处理，通常会开启多个线程。
但是，我们不能让大量的线程同时运行处理任务。（占用过多的资源）
这个时候，如果有需要开启线程处理任务的情况，我们就会使用线程队列。
线程队列会依照次序来启动线程，并且处理对应的任务。

当然队列还有很多其他应用，我们后续的很多算法中也会用到队列（比如二叉树的层序遍历）。

队列如何实现呢？

我们一起来研究一下队列的实现。

队列类的创建

队列的实现和栈一样，有两种方案：

基于数组实现
基于链表实现

我们需要创建自己的类，来实现一个队列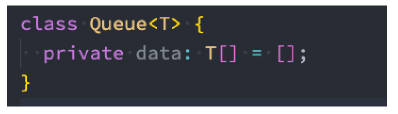

代码解析：

我们创建了一个 Queue 的类，用户创建队列的类，并且是一个泛型类。
在类中，定义了一个变量，这个变量可以用于保存当前队列对象中所有的元素。（和创建栈非常相似）
这个变量是一个数组类型。
- 我们之后在队列中添加元素或者删除元素，都是在这个数组中完成的。
队列和栈一样，有一些相关的操作方法，通常无论是什么语言，操作都是比较类似的。

队列的常见操作

队列有哪些常见的操作呢？

enqueue(element)：向队列尾部添加一个（或多个）新的项。
dequeue(): 移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
front/peek(): 返回队列中第一个元素 - 最先被添加，也将是最先被移除的元素。
- 队列不做任何变动（不移除元素，只返回元素信息 - 与 Stack 类的 peek 方法非常类型）。
isEmpty()：如果队列中不包含任何元素，返回 true，否则返回 false。
size(): 返回队列包含的元素个数，与数组的 length 属性类似。

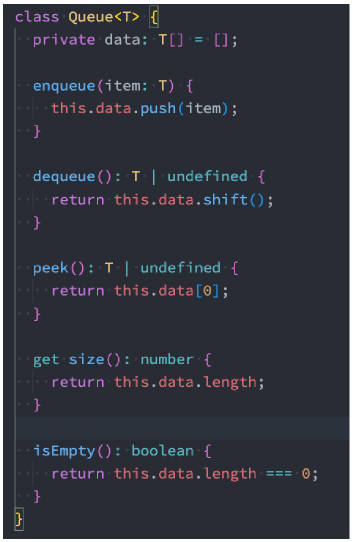
现在，我们来实现这些方法。

其实和栈中方法的实现非常相似，因为我们的队列也是基于数组的

IQueue.ts

TypeScript

interface IQueue<T> {
  enqueue(element: T): void
  dequeue(): T | undefined
  peek(): T | undefined
  isEmpty(): boolean
  get size(): number
}

export default IQueue

01_实现队列结构 Queue.ts

typescript

import IQueue from "./IQueue";
class ArrayQueue<T> implements IQueue<T> {
  private data: T[] = [];

  enqueue(element: T): void {
    this.data.push(element);
  }

  dequeue(): T | undefined {
    return this.data.shift();
  }

  peek(): T | undefined {
    return this.data[0];
  }

  isEmpty(): boolean {
    return this.data.length === 0;
  }

  get size(): number {
    return this.data.length;
  }
}

export default ArrayQueue;

类型抽取 tepes/IList.ts

typescript

interface IList<T> {
  peek(): T | undefined;
  isEmpty(): boolean;
  size(): number;
}

IQueue.ts

typescript

interface IQueue<T> extends IList<T> {
  enqueue(element: T): void;
  dequeue(): T | undefined;
}

IStack.ts

typescript

interface IStack<T> extends IList<T> {
  push(element: T): void;
  pop(): T | undefined;
}

击鼓传花

击鼓传花是一个常见的面试算法题：使用队列可以非常方便的实现最终的结果。

原游戏规则：

班级中玩一个游戏，所有学生围城一圈，从某位同学手里开始向旁边的同学传一束花。
这个时候某个人（比如班长），在击鼓，鼓声停下的一刻，花落在谁手里，谁就出来表演节目。

修改游戏规则：

我们来修改一下这个游戏规则。
几个朋友一起玩一个游戏，围成一圈，开始数数，数到某个数字的人自动淘汰。
最后剩下的这个人会获得胜利，请问最后剩下的是原来在哪一个位置上的人？

封装一个基于队列的函数：

参数：所有参与人的姓名，基于的数字；
结果：最终剩下的一人的姓名；

击鼓传花的实现

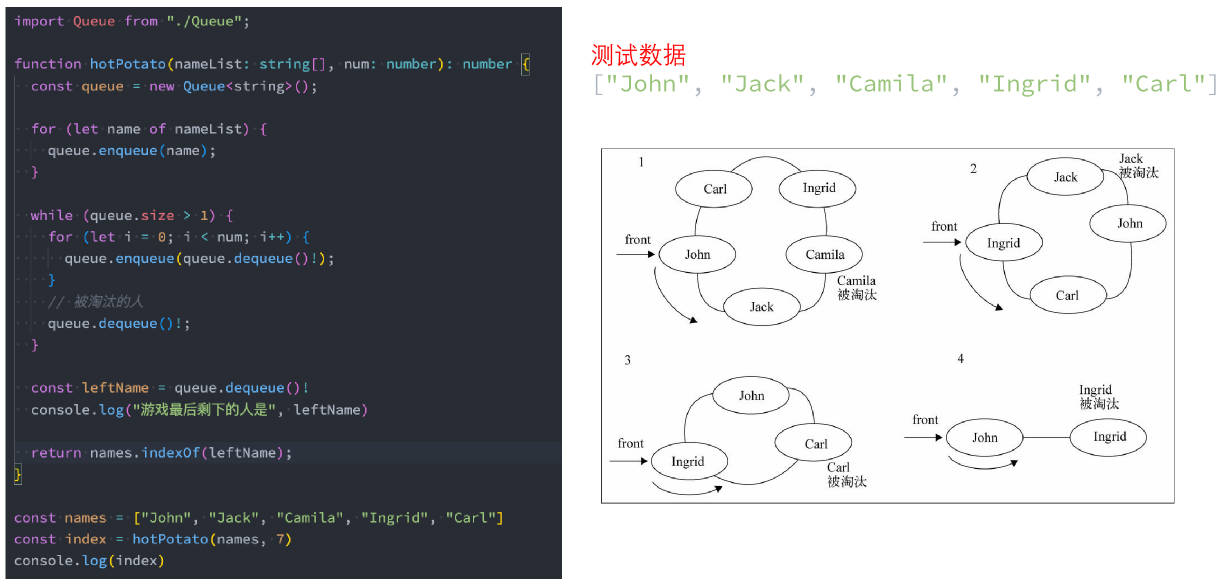
02_面试题 1-击鼓传花.ts

typescript

import ArrayQueue from "./01_实现队列结构Queue";

function hotPotato(names: string[], num: number): number {
  if (!names.length) return -1;
  // 1.创建队列结构
  const queue = new ArrayQueue<string>();

  // 2.将所有的name入队操作
  for (const name of names) {
    queue.enqueue(name);
  }

  // 3.淘汰的规则
  while (queue.size() > 1) {
    // 1/2不淘汰
    for (let i = 1; i < num; i++) {
      const name = queue.dequeue();
      if (name) queue.enqueue(name);
    }
    // 3淘汰
    queue.dequeue();
  }

  // 4.取出最后一个人
  const leftName = queue.dequeue()!;
  const index = names.indexOf(leftName);
  return index;
}

const leftName = hotPotato(["why", "james", "kobe", "curry"], 3);
console.log(leftName);

什么是约瑟夫环问题（历史）？

阿桥问题（有时也称为约瑟夫斯置换），是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。

人们站在一个等待被处决的圈子里。
计数从圆圈中的指定点开始，并沿指定方向围绕圆圈进行。
在跳过指定数量的人之后，处刑下一个人。
对剩下的人重复该过程，从下一个人开始，朝同一方向跳过相同数量的人，直到只剩下一个人，并被释放。
在给定数量的情况下，站在第几个位置可以避免被处决？

这个问题是以弗拉维奥·约瑟夫命名的，他是 1 世纪的一名犹太历史学家。

他在自己的日记中写道，他和他的 40 个战友被罗马军队包围在洞中。
他们讨论是自杀还是被俘，最终决定自杀、并以抽签的方式决定谁杀掉谁。

约瑟夫环问题 - 字节、阿里、谷歌等面试题

击鼓传花和约瑟夫环其实是同一类问题，这种问题还会有其他解法（后续讲解）同样的题目在 Leetcode 上也有：

https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
0,1,...,n-1 这 n 个数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。
例如，0、1、2、3、4 这 5 个数字组成一个圆圈，从数字 0 开始每次删除第 3 个数字，则删除的前 4 个数字依次是 2、0、4、1，因此最后剩下的数字是 3。

03_面试题 2-约瑟夫环.ts

typescript

import ArrayQueue from "./01_实现队列结构Queue";

function lastRemaining(n: number, m: number) {
  // 1.创建队列
  const queue = new ArrayQueue<number>();

  // 2.将所有的数字加入到队列中
  for (let i = 0; i < n; i++) {
    queue.enqueue(i);
  }

  // 3.判断队列中是否还有数字
  while (queue.size() > 1) {
    for (let i = 1; i < m; i++) {
      queue.enqueue(queue.dequeue()!);
    }
    queue.dequeue();
  }

  return queue.dequeue()!;
}

console.log(lastRemaining(5, 3)); // 3
console.log(lastRemaining(10, 17)); // 2

动态规划（先了解）

typescript

function lastRemaining(n: number, m: number) {
  let position = 0;
  for (let i = 2; i <= n; i++) {
    position = (position + m) % i;
  }
  return position;
}

队列结构（Queue） ​

认识队列 ​

生活中的队列 ​

开发中队列的应用 ​

队列类的创建 ​

队列的常见操作 ​

击鼓传花 ​

击鼓传花的实现 ​

什么是约瑟夫环问题（历史）？ ​

约瑟夫环问题 - 字节、阿里、谷歌等面试题 ​

队列结构（Queue）

认识队列

生活中的队列

开发中队列的应用

队列类的创建

队列的常见操作

击鼓传花

击鼓传花的实现

什么是约瑟夫环问题（历史）？

约瑟夫环问题 - 字节、阿里、谷歌等面试题