堆结构（Heap）

什么是堆（Heap）结构？

堆是也是一种非常常见的数据结构，但是相对于前面的数据结构来说，要稍微难理解一点。

堆的本质是一种特殊的树形数据结构，使用完全二叉树来实现：

堆可以进行很多分类，但是平时使用的基本都是二叉堆；
二叉堆又可以划分为最大堆和最小堆；

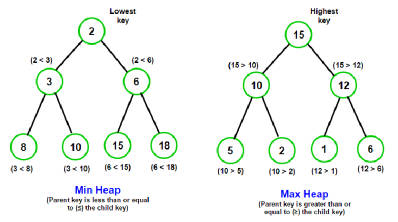
最大堆和最小堆：

最小堆：堆中每一个节点都小于等于（<=）它的子节点；
最大堆：堆中每一个节点都大于等于（>=）它的子节点；

为什么需要堆（Heap）结构？

但是这个堆东西有什么意义呢？

对于每一个新的数据结构，我们都需要搞清楚为什么需要它，这是我们能够记住并且把握它的关键。
它到底帮助我们解决了什么问题？

如果有一个集合，我们希望获取其中的最大值或者最小值，有哪些方案呢？

数组/链表：获取最大或最小值是 O(n)级别的；
✓ 可以进行排序，但是我们只是获取最大值或者最小值而已
✓ 排序本身就会消耗性能；
哈希表：不需要考虑了；
二叉搜索树：获取最大或最小值是 O(logn)级别的；
✓ 但是二叉搜索树操作较为复杂，并且还要维护树的平衡时才是 O(logn)级别；

这个时候需要一种数据结构来解决这个问题，就是堆结构。

认识堆（Heap）结构

堆结构通常是用来解决 Top K 问题的：

Top K 问题是指在一组数据中，找出最前面的 K 个最大/最小的元素；
常用的解决方案有使用排序算法、快速选择算法、堆结构等；

但是我们还是不知道具体长什么样子，以及它是如何实现出来的：

二叉堆用树形结构表示出来是一颗完全二叉树；
通常在实现的时候我们底层会使用数组来实现；

每个节点在数组中对应的索引 i（index）有如下的规律：

如果 i = 0 ，它是根节点；
父节点的公式：floor( (i – 1) / 2 )
左子节点：2i + 1
右子节点：2i + 2

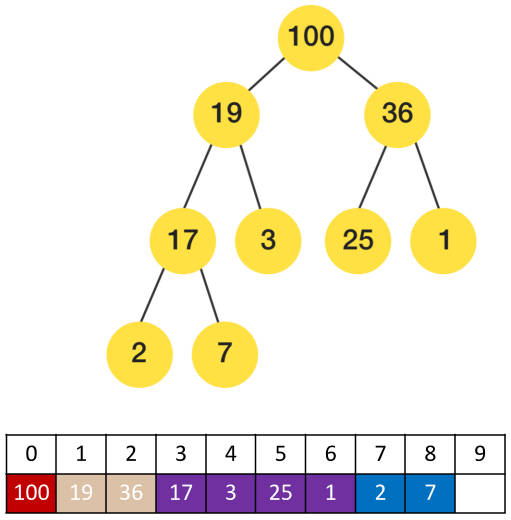
堆结构的性质

堆结构的设计

接下来，让我们对堆结构进行设计，看看需要有哪些属性和方法。

常见的属性：

data：存储堆中的元素，通常使用数组来实现。
size：堆中当前元素的数量。

常见的方法：

insert(value)：在堆中插入一个新元素。
extract/delete()：从堆中删除最大/最小元素。
peek()：返回堆中的最大/最小元素。
isEmpty()：判断堆是否为空。
build_heap(list)：通过一个列表来构造堆。

那么接下来我们就来实现这个堆结构吧！

堆结构的封装

封装 Heap 的类：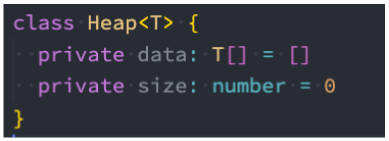

这个堆结构里面只包含了两个属性：data 和 size

data是一个泛型数组，存储堆中的元素；
size是当前堆中元素的数量。

typescript

// 09_堆结构HEAP/01_堆结构Heap(封装).ts

class Heap<T> {
  // 属性
  private data: T[] = [];
  private length: number = 0;

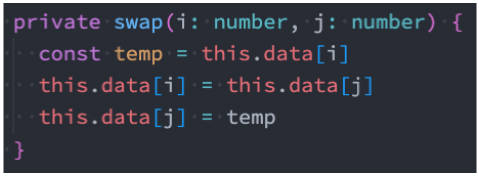
  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  // 方法
  insert(value: T) {}
  extract(): T | undefined {
    return undefined;
  }

  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {}
}

export {};

insert 插入元素

如果你想实现一个最大堆，那么可以从实现“insert”方法开始。

因为每次插入元素后，需要对堆进行重构，以维护最大堆的性质。
这种策略叫做上滤（percolate up， percolate [ˈpɜːkəleɪt] 是过滤的意思）。

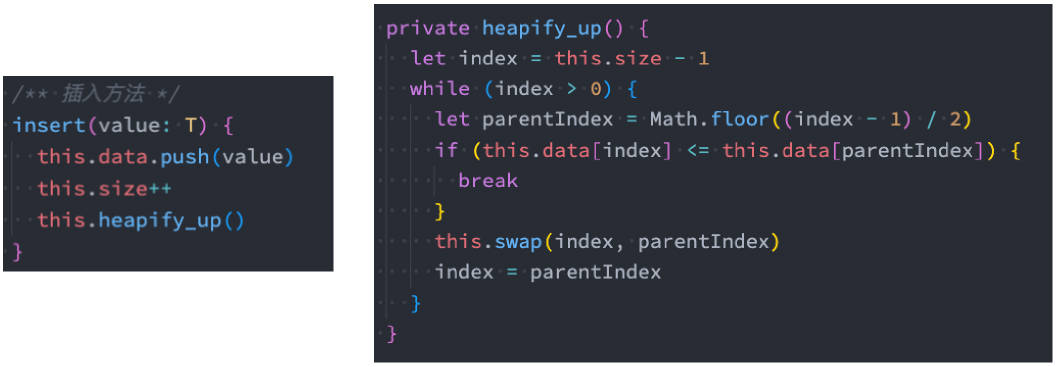
数据模拟

typescript

// 09_堆结构HEAP/02_堆结构Heap(插入).ts

class Heap<T> {
  // 属性
  data: T[] = [];
  private length: number = 0;

  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  // 方法
  insert(value: T) {
    // 1.将元素放到数组的尾部
    this.data.push(value);
    this.length++;

    // 2.维护最大堆的特性(最后位置的元素需要进行上滤操作)
    this.heapify_up();
  }

  heapify_up() {
    let index = this.length - 1;
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      if (this.data[index] <= this.data[parentIndex]) {
        break;
      }
      this.swap(index, parentIndex);
      index = parentIndex;
    }
  }

  extract(): T | undefined {
    return undefined;
  }

  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {}
}

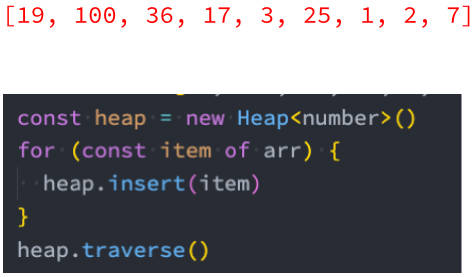
const arr = [19, 100, 36, 17, 3, 25, 1, 2, 7];

const heap = new Heap<number>();
for (const item of arr) {
  heap.insert(item);
}
console.log(heap.data);

heap.insert(133);
console.log(heap.data);
heap.insert(65);
console.log(heap.data);

console.log(heap.extract());

export {};

数据结构可视化

在线数据结构演练：

插入元素 insert

如果我们现在有这样一个结构的最大堆：插入 120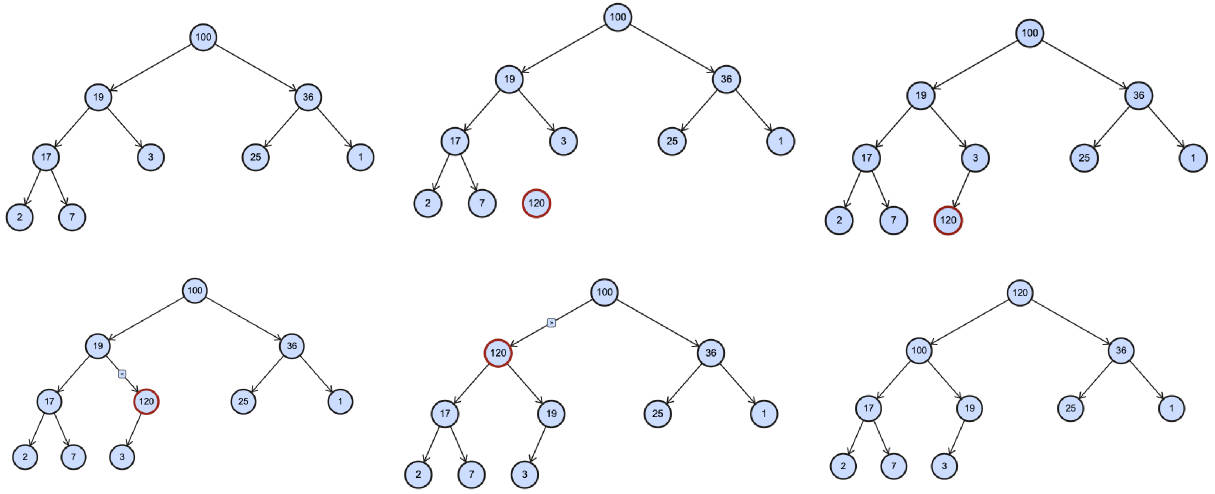

delete 删除元素

删除操作也需要考虑在删除元素后的操作：

因为每次删除元素后，需要对堆进行重构，以维护最大堆的性质。
这种向下替换元素的策略叫作下滤（percolate down）。

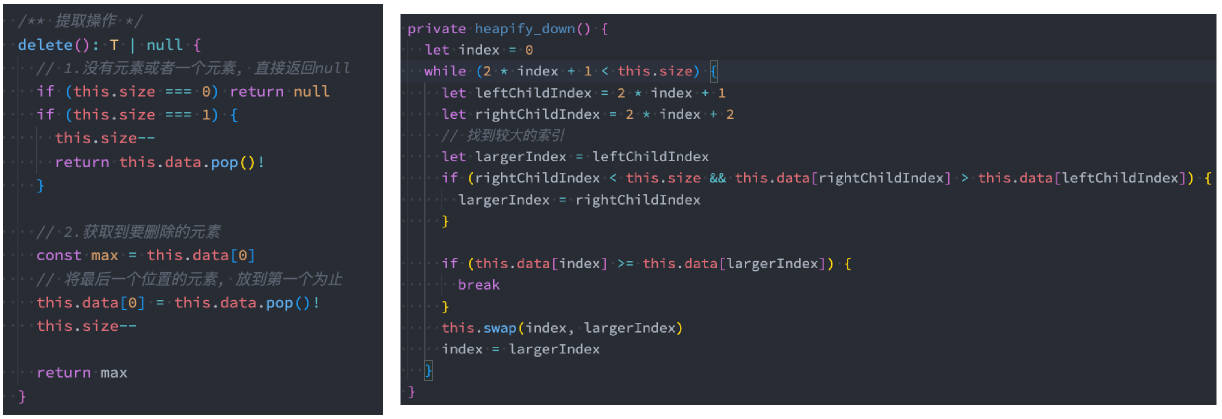
typescript

// 09_堆结构HEAP/03_堆结构Heap(删除).ts

class Heap<T> {
  // 属性
  data: T[] = [];
  private length: number = 0;

  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  // 方法
  /** 插入操作 */
  insert(value: T) {
    // 1.将元素放到数组的尾部
    this.data.push(value);
    this.length++;

    // 2.维护最大堆的特性(最后位置的元素需要进行上滤操作)
    this.heapify_up();
  }

  private heapify_up() {
    let index = this.length - 1;
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      if (this.data[index] <= this.data[parentIndex]) {
        break;
      }
      this.swap(index, parentIndex);
      index = parentIndex;
    }
  }

  /** 提取操作 */
  extract(): T | undefined {
    // 1.判断元素的个数为0或者1的情况
    if (this.length === 0) return undefined;
    if (this.length === 1) {
      this.length--;
      return this.data.pop()!;
    }

    // 2.提取并且需要返回的最大值
    const topValue = this.data[0];
    this.data[0] = this.data.pop()!;
    this.length--;

    // 3.维护最大堆的特性: 下滤操作
    this.heapify_down();

    return topValue;
  }

  private heapify_down() {
    // 3.1.定义索引位置
    let index = 0;

    while (2 * index + 1 < this.length) {
      // 3.2.找到左右子节点
      let leftChildIndex = 2 * index + 1;
      let rightChildIndex = leftChildIndex + 1;

      // 3.3.找到左右子节点较大的值
      let largerIndex = leftChildIndex;
      if (
        rightChildIndex < this.length &&
        this.data[rightChildIndex] > this.data[leftChildIndex]
      ) {
        largerIndex = rightChildIndex;
      }

      // 3.4.较大的值和index位置进行比较
      if (this.data[index] >= this.data[largerIndex]) {
        break;
      }

      // 3.5.交换位置
      this.swap(index, largerIndex);
      index = largerIndex;
    }
  }

  /** 其他方法 */
  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {}
}

const arr = [19, 100, 36, 17, 3, 25, 1, 2, 7];

const heap = new Heap<number>();
for (const item of arr) {
  heap.insert(item);
}
console.log(heap.data);

while (!heap.isEmpty()) {
  console.log(heap.extract());
}

export {};

提取操作 extract、delete

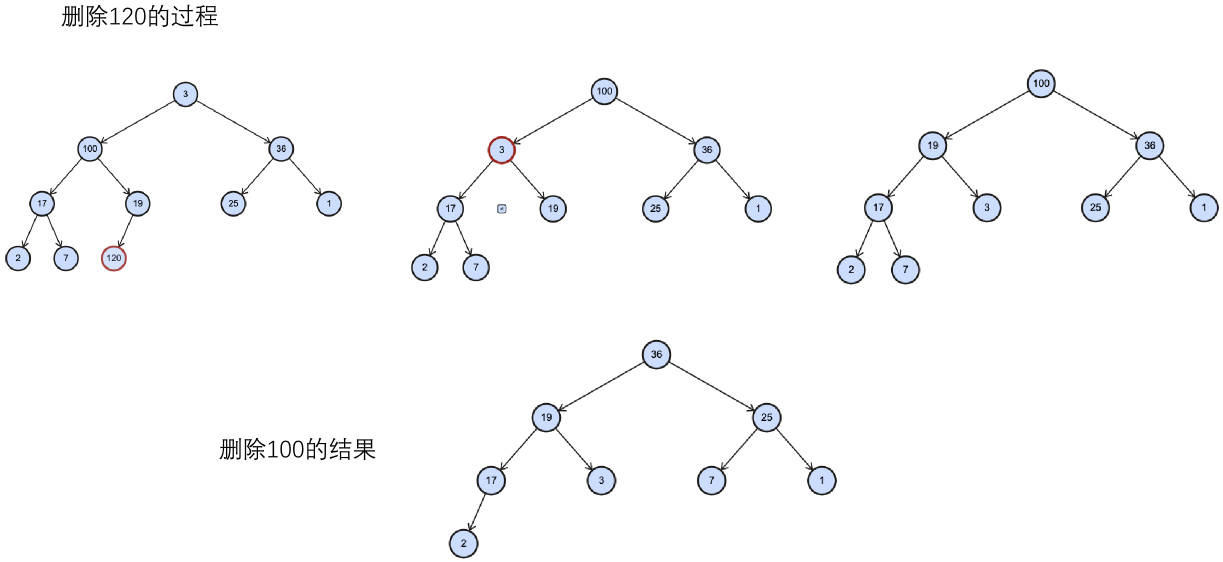
其他方法的实现

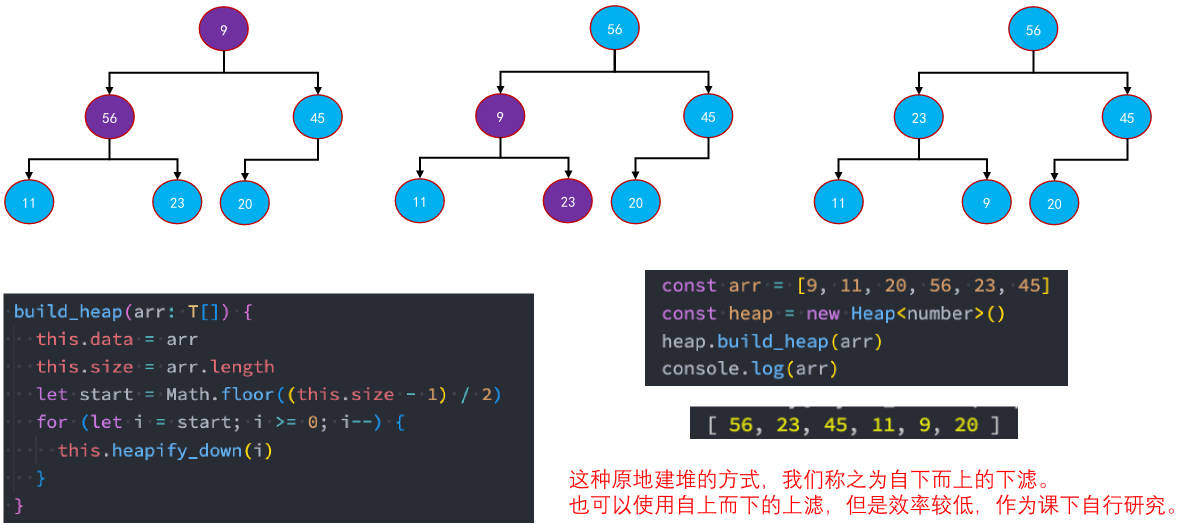
原地建堆

“原地建堆” （In-place heap construction.）是指建立堆的过程中，不使用额外的内存空间，直接在原有数组上进行操作。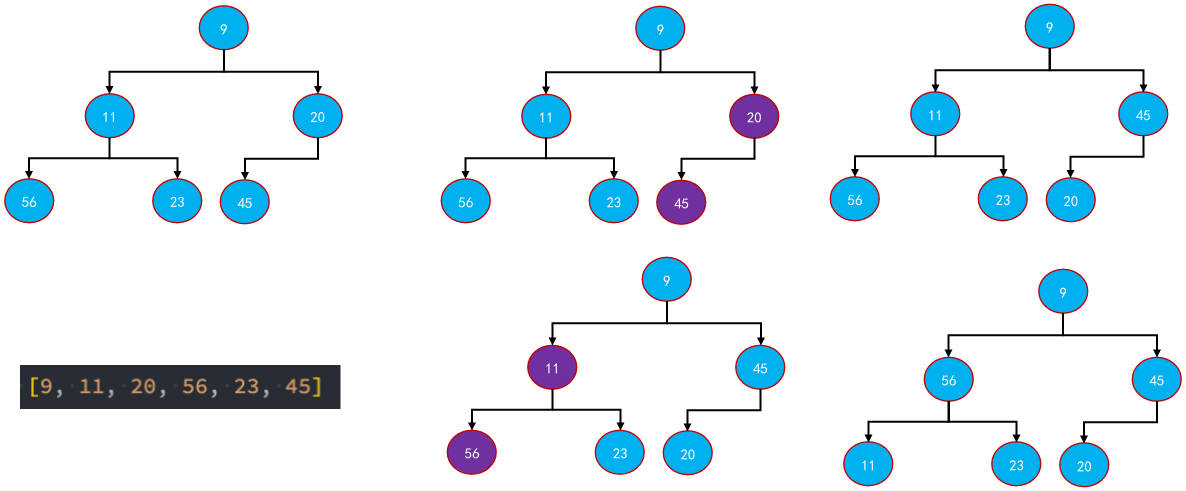

typescript

// 09_堆结构HEAP/04_堆结构Heap(原地建堆).ts

class Heap<T> {
  // 属性
  data: T[] = [];
  private length: number = 0;

  constructor(arr: T[] = []) {
    this.buildHeap(arr);
  }

  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  // 方法
  /** 插入操作 */
  insert(value: T) {
    // 1.将元素放到数组的尾部
    this.data.push(value);
    this.length++;

    // 2.维护最大堆的特性(最后位置的元素需要进行上滤操作)
    this.heapify_up();
  }

  private heapify_up() {
    let index = this.length - 1;
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      if (this.data[index] <= this.data[parentIndex]) {
        break;
      }
      this.swap(index, parentIndex);
      index = parentIndex;
    }
  }

  /** 提取操作 */
  extract(): T | undefined {
    // 1.判断元素的个数为0或者1的情况
    if (this.length === 0) return undefined;
    if (this.length === 1) {
      this.length--;
      return this.data.pop()!;
    }

    // 2.提取并且需要返回的最大值
    const topValue = this.data[0];
    this.data[0] = this.data.pop()!;
    this.length--;

    // 3.维护最大堆的特性: 下滤操作
    this.heapify_down(0);

    return topValue;
  }

  private heapify_down(start: number) {
    // 3.1.定义索引位置
    let index = start;

    while (2 * index + 1 < this.length) {
      // 3.2.找到左右子节点
      let leftChildIndex = 2 * index + 1;
      let rightChildIndex = leftChildIndex + 1;

      // 3.3.找到左右子节点较大的值
      let largerIndex = leftChildIndex;
      if (
        rightChildIndex < this.length &&
        this.data[rightChildIndex] > this.data[leftChildIndex]
      ) {
        largerIndex = rightChildIndex;
      }

      // 3.4.较大的值和index位置进行比较
      if (this.data[index] >= this.data[largerIndex]) {
        break;
      }

      // 3.5.交换位置
      this.swap(index, largerIndex);
      index = largerIndex;
    }
  }

  /** 其他方法 */
  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {
    // 1.使用arr的值: 数组/长度
    this.data = arr;
    this.length = arr.length;

    // 2.从第一个非叶子节点, 开始进行下滤操作
    const start = Math.floor(this.length / 2 - 1);
    for (let i = start; i >= 0; i--) {
      this.heapify_down(i);
    }
  }
}

const arr = [9, 11, 20, 56, 23, 45];
const heap = new Heap<number>(arr);

// heap.buildHeap(arr)
console.log(arr);
console.log(heap.extract());

export {};

typescript

// 09_堆结构HEAP/05_堆结构Heap(最小堆).ts

class Heap<T> {
  // 属性
  data: T[] = [];
  private length: number = 0;

  constructor(arr: T[] = []) {
    if (arr.length === 0) return;
    this.buildHeap(arr);
  }

  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  // 方法
  /** 插入操作 */
  insert(value: T) {
    // 1.将元素放到数组的尾部
    this.data.push(value);
    this.length++;

    // 2.维护最大堆的特性(最后位置的元素需要进行上滤操作)
    this.heapify_up();
  }

  private heapify_up() {
    let index = this.length - 1;
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      if (this.data[parentIndex] <= this.data[index]) {
        break;
      }
      this.swap(index, parentIndex);
      index = parentIndex;
    }
  }

  /** 提取操作 */
  extract(): T | undefined {
    // 1.判断元素的个数为0或者1的情况
    if (this.length === 0) return undefined;
    if (this.length === 1) {
      this.length--;
      return this.data.pop()!;
    }

    // 2.提取并且需要返回的最大值
    const topValue = this.data[0];
    this.data[0] = this.data.pop()!;
    this.length--;

    // 3.维护最大堆的特性: 下滤操作
    this.heapify_down(0);

    return topValue;
  }

  private heapify_down(start: number) {
    // 3.1.定义索引位置
    let index = start;

    while (2 * index + 1 < this.length) {
      // 3.2.找到左右子节点
      let leftChildIndex = 2 * index + 1;
      let rightChildIndex = leftChildIndex + 1;

      // 3.3.找到左右子节点较大的值
      let largerIndex = leftChildIndex;
      if (
        rightChildIndex < this.length &&
        this.data[rightChildIndex] <= this.data[leftChildIndex]
      ) {
        largerIndex = rightChildIndex;
      }

      // 3.4.较大的值和index位置进行比较
      if (this.data[index] <= this.data[largerIndex]) {
        break;
      }

      // 3.5.交换位置
      this.swap(index, largerIndex);
      index = largerIndex;
    }
  }

  /** 其他方法 */
  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {
    // 1.使用arr的值: 数组/长度
    this.data = arr;
    this.length = arr.length;

    // 2.从第一个非叶子节点, 开始进行下滤操作
    const start = Math.floor((this.length - 1) / 2);
    for (let i = start; i >= 0; i--) {
      this.heapify_down(i);
    }
  }
}

const arr = [19, 100, 36, 17, 3, 25];
// 1.测试插入操作
// const heap = new Heap<number>()
// for (const item of arr) {
//   heap.insert(item)
// }
// console.log(heap.data)

// 2.测试提取/删除操作
// while (!heap.isEmpty()) {
//   console.log(heap.extract())
// }

// 3.测试批量建堆
const heap = new Heap<number>(arr);
console.log(arr);
console.log(heap.extract());

export {};

typescript

// 09_堆结构HEAP/06_堆结构Heap(二叉堆).ts

import { cbtPrint } from "hy-algokit";

export default class Heap<T> {
  // 属性
  private data: T[] = [];
  private length: number = 0;
  private isMax: boolean;

  constructor(arr: T[] = [], isMax = true) {
    this.isMax = isMax;
    if (arr.length === 0) return;
    this.buildHeap(arr);
  }

  // 私有工具方法
  private swap(i: number, j: number) {
    const temp = this.data[i];
    this.data[i] = this.data[j];
    this.data[j] = temp;
  }

  private compare(i: number, j: number): boolean {
    if (this.isMax) {
      return this.data[i] >= this.data[j];
    } else {
      return this.data[i] <= this.data[j];
    }
  }

  // 方法
  /** 插入操作 */
  insert(value: T) {
    // 1.将元素放到数组的尾部
    this.data.push(value);
    this.length++;

    // 2.维护最大堆的特性(最后位置的元素需要进行上滤操作)
    this.heapify_up();
  }

  private heapify_up() {
    let index = this.length - 1;
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      if (this.compare(parentIndex, index)) {
        break;
      }
      this.swap(index, parentIndex);
      index = parentIndex;
    }
  }

  /** 提取操作 */
  extract(): T | undefined {
    // 1.判断元素的个数为0或者1的情况
    if (this.length === 0) return undefined;
    if (this.length === 1) {
      this.length--;
      return this.data.pop()!;
    }

    // 2.提取并且需要返回的最大值
    const topValue = this.data[0];
    this.data[0] = this.data.pop()!;
    this.length--;

    // 3.维护最大堆的特性: 下滤操作
    this.heapify_down(0);

    return topValue;
  }

  private heapify_down(start: number) {
    // 3.1.定义索引位置
    let index = start;

    while (2 * index + 1 < this.length) {
      // 3.2.找到左右子节点
      let leftChildIndex = 2 * index + 1;
      let rightChildIndex = leftChildIndex + 1;

      // 3.3.找到左右子节点较大的值
      let largerIndex = leftChildIndex;
      if (
        rightChildIndex < this.length &&
        this.compare(rightChildIndex, leftChildIndex)
      ) {
        largerIndex = rightChildIndex;
      }

      // 3.4.较大的值和index位置进行比较
      if (this.compare(index, largerIndex)) {
        break;
      }

      // 3.5.交换位置
      this.swap(index, largerIndex);
      index = largerIndex;
    }
  }

  /** 其他方法 */
  peek(): T | undefined {
    return this.data[0];
  }

  size() {
    return this.length;
  }

  isEmpty() {
    return this.length === 0;
  }

  buildHeap(arr: T[]) {
    // 1.使用arr的值: 数组/长度
    this.data = arr;
    this.length = arr.length;

    // 2.从第一个非叶子节点, 开始进行下滤操作
    const start = Math.floor((this.length - 1) / 2);
    for (let i = start; i >= 0; i--) {
      this.heapify_down(i);
    }
  }

  print() {
    cbtPrint(this.data);
  }
}

const arr = [19, 100, 36, 17, 3, 25];
// 1.测试插入操作
// const heap = new Heap<number>([], false)
// for (const item of arr) {
//   heap.insert(item)
// }
// console.log(heap.data)

// // 2.测试提取/删除操作
// while (!heap.isEmpty()) {
//   console.log(heap.extract())
// }

// 3.测试批量建堆
const heap = new Heap<number>(arr, false);
// console.log(arr)
// cbtPrint(arr)
// console.log(heap.extract())

// heap.print()

export {};

堆结构（Heap） ​

什么是堆（Heap）结构？ ​

为什么需要堆（Heap）结构？ ​

认识堆（Heap）结构 ​

堆结构的性质 ​

堆结构的设计 ​

堆结构的封装 ​

insert 插入元素 ​

数据模拟 ​

数据结构可视化 ​

插入元素 insert ​

delete 删除元素 ​

提取操作 extract、delete ​

其他方法的实现 ​

原地建堆 ​

堆结构（Heap）

什么是堆（Heap）结构？

为什么需要堆（Heap）结构？

认识堆（Heap）结构

堆结构的性质

堆结构的设计

堆结构的封装

insert 插入元素

数据模拟

数据结构可视化

插入元素 insert

delete 删除元素

提取操作 extract、delete

其他方法的实现

原地建堆