大厂面试题 - Leetcode

14.最长公共前缀（Google、字节、亚马逊等）

14.最长公共前缀（Longest Common Prefix）

• https://leetcode.cn/problems/longest-common-prefix/ 题目：
• 编写一个函数来查找字符串数组中的最长公共前缀。
• 如果不存在公共前缀，返回空字符串""。

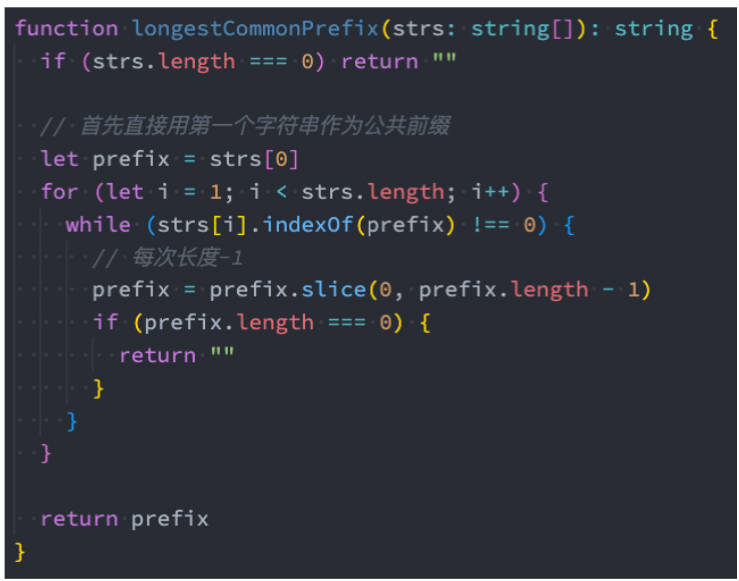
14.最长公共前缀 – 代码实现

3.无重复字符的最长子串（字节、亚马逊、阿里等）

3.无重复字符的最长子串

• https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/

题目：

• 给定一个字符串s，请你找出其中不含有重复字符的 最长子串 的长度。

3.无重复字符的最长子串 – 代码实现

5.最长回文子串（亚马逊、华为、苹果等）

最长回文子串

• https://leetcode.cn/problems/longest-palindromic-substring/description/

题目：

• 给你一个字符串 s，找到 s 中最长的回文子串。
• 如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

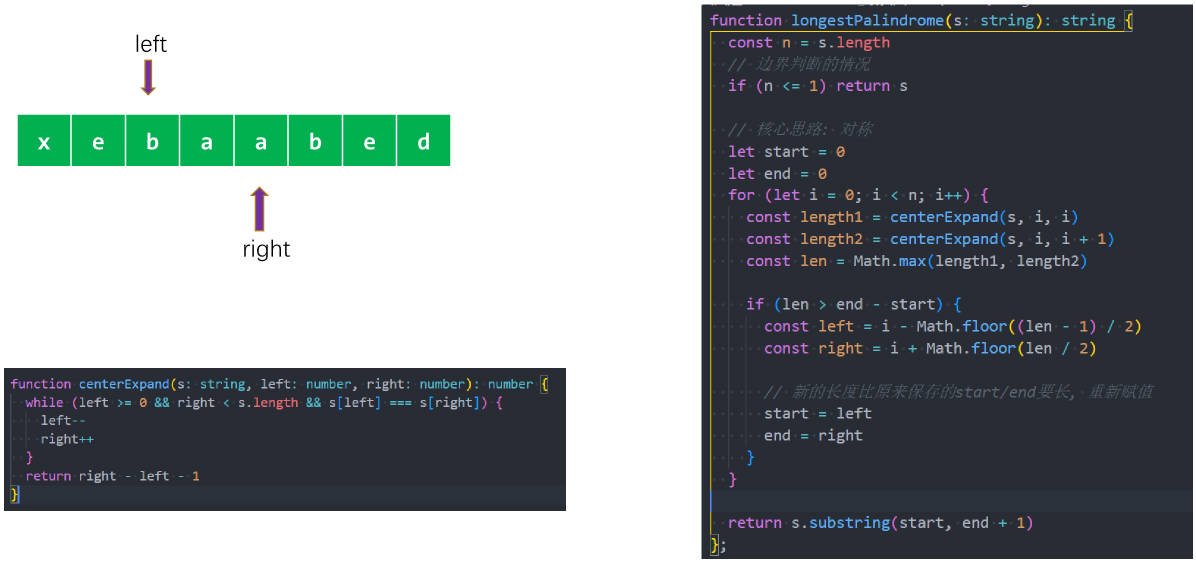
5.最长回文子串–代码实现

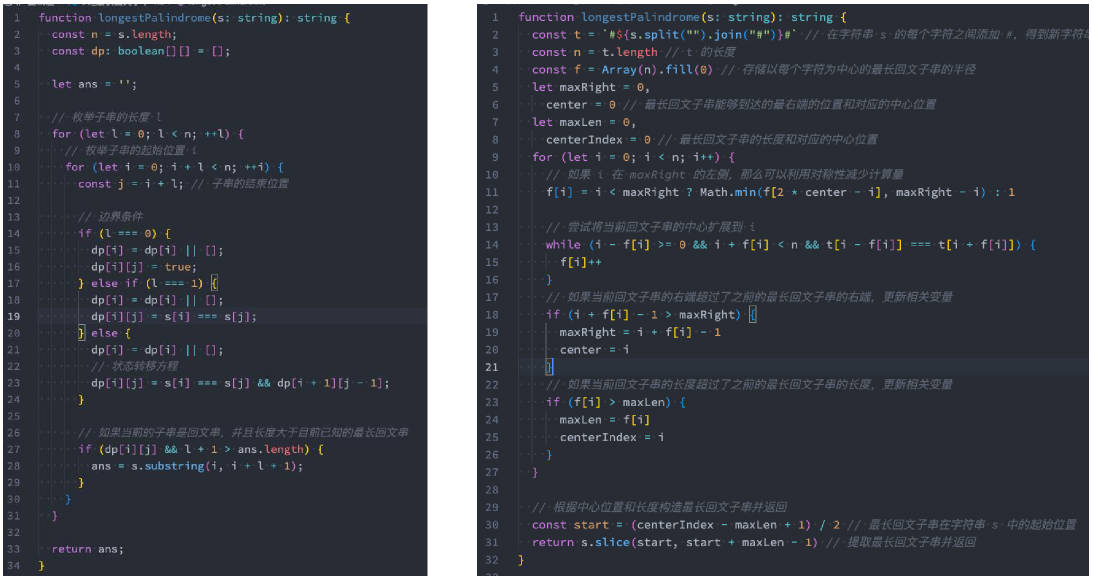
动态规划 – Manacher算法（课下扩展）

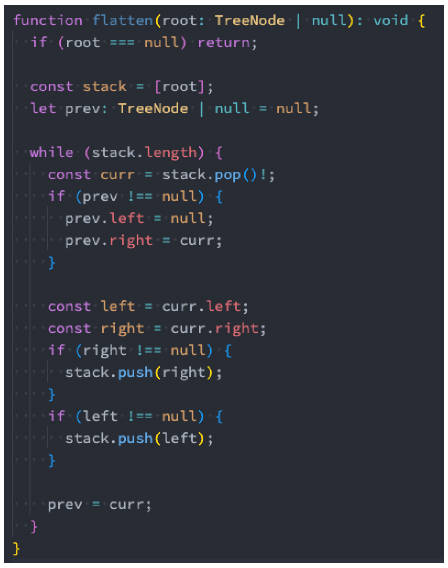
114.二叉树展开为链表（微软、字节、谷歌）

114.二叉树展开为链表

• https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/

题目：

• 给你二叉树的根结点 root，请你将它展开为一个单链表：
  • 展开后的单链表应该同样使用 TreeNode，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null。
  • 展开后的单链表应该与二叉树先序遍历顺序相同。

114.二叉树展开为链表–代码实现

可以使用栈结构：

• 将当前节点的右子树和左子树依次压入栈中。
• 然后再取出栈顶元素，将其左子树设为空，右子树设为栈顶元素。
• 再继续将新的右子树和左子树压入栈中，重复这个过程直到栈为空。

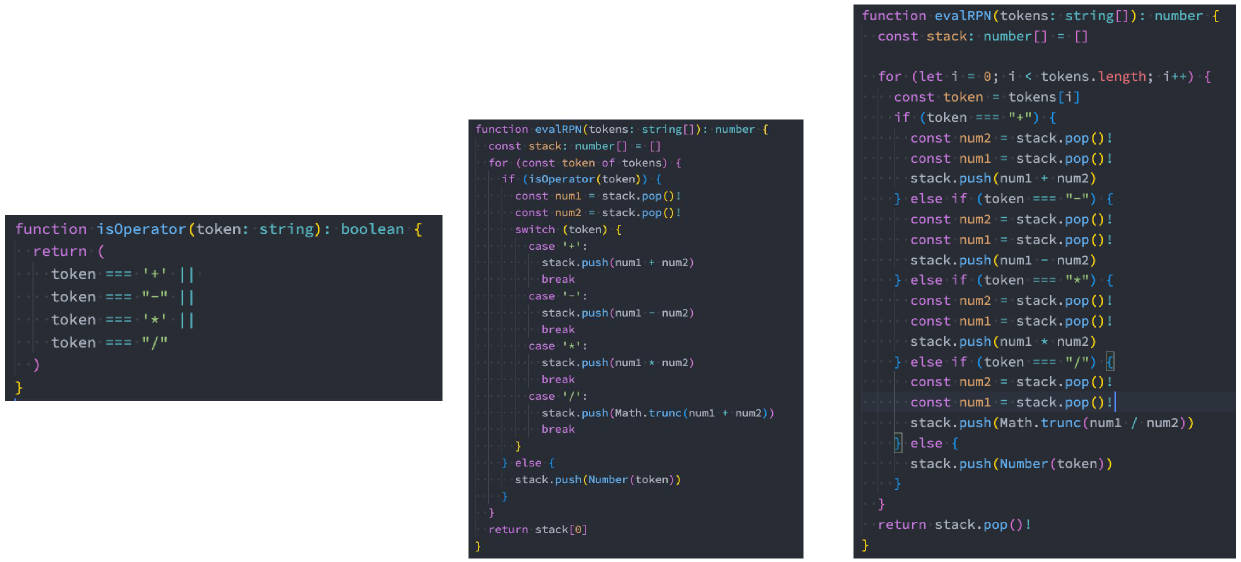
150.逆波兰表达式求值（亚马逊、谷歌、腾讯等）

150.逆波兰表达式求值

• https://leetcode.cn/problems/evaluate-reverse-polish-notation/description/

题目：

• 给你一个字符串数组tokens，表示一个根据逆波兰表示法表示的算术表达式。
• 请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为'+'、'-'、'*'和'/'。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32位 整数表示。

150.逆波兰表达式求值 – 代码实现

使用了一个栈来存储数字和运算符。

• 遍历 tokens 数组，遇到数字时将其压入栈中，遇到运算符时从栈中弹出两个数字并进行相应的计算，将计算结果再压入栈中。
• 最后栈中剩下的数字就是表达式的值。

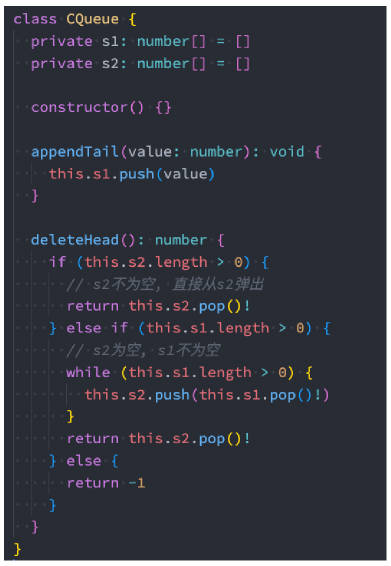
剑指 Offer 09.用两个栈实现队列（字节、百度等）

剑指 Offer 09.用两个栈实现队列：

• https://leetcode.cn/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof/description/

题目：

• 用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回-1 )

用两个栈实现队列 – 代码实现

使用两个栈 s1 和 s2：s1 用来插入元素，s2 用来删除元素

• 其中插入元素只需要将元素插入 s1 即可
• 删除元素则需要分情况：
  • 如果 s2 不为空，直接弹出s2 的栈顶元素；
  • 如果 s2 为空，将 s1 中的元素逐个弹出并压入 s2，然后弹出 s2 的栈顶元素；

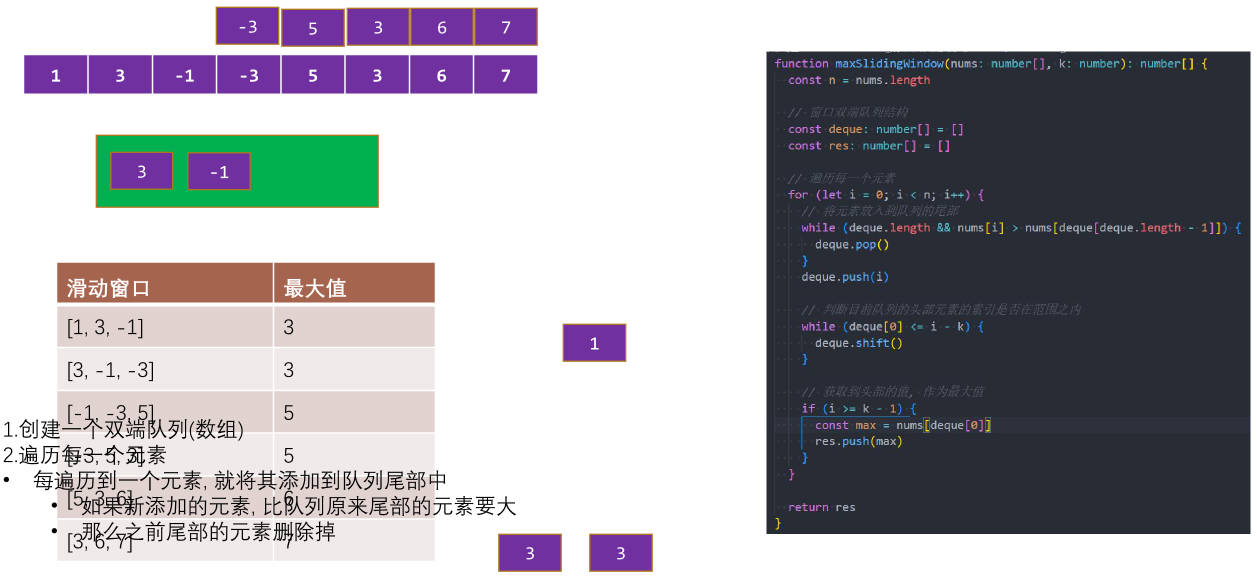
239.滑动窗口最大值（亚马逊、谷歌、字节等）

239.滑动窗口最大值

• https://leetcode.cn/problems/sliding-window-maximum/description/

首先，我们需要定义一个双端队列 deque 用来存储下标，一个空数组 res 用来存储结果。

接着，我们遍历整个数组，对于当前的数字 nums[i]，如果双端队列 deque 不为空，并且当前数字 nums[i] 大于等于队列末尾的数字，则我们弹出队列末尾的数字，直到队列为空或者当前数字 nums[i] 小于队列末尾的数字。这样可以保证队列中的数字是单调递减的。然后，我们将当前数字的下标 i 入队。

接下来，我们需要保证队列中的数字是在滑动窗口范围内的。如果队列头部的数字的下标小于等于 i-k，说明这个数字已经不在滑动窗口内，我们需要弹出队列头部的数字。

最后，如果当前下标 i 大于等于 k - 1，我们将队列头部数字所对应的 nums 中的数字加入到结果数组 res 中。

双端队列的实现

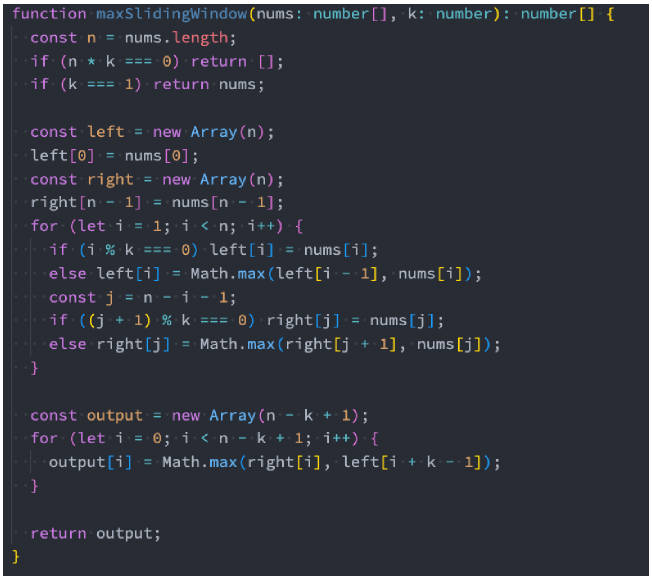
动态规划实现（课下扩展）

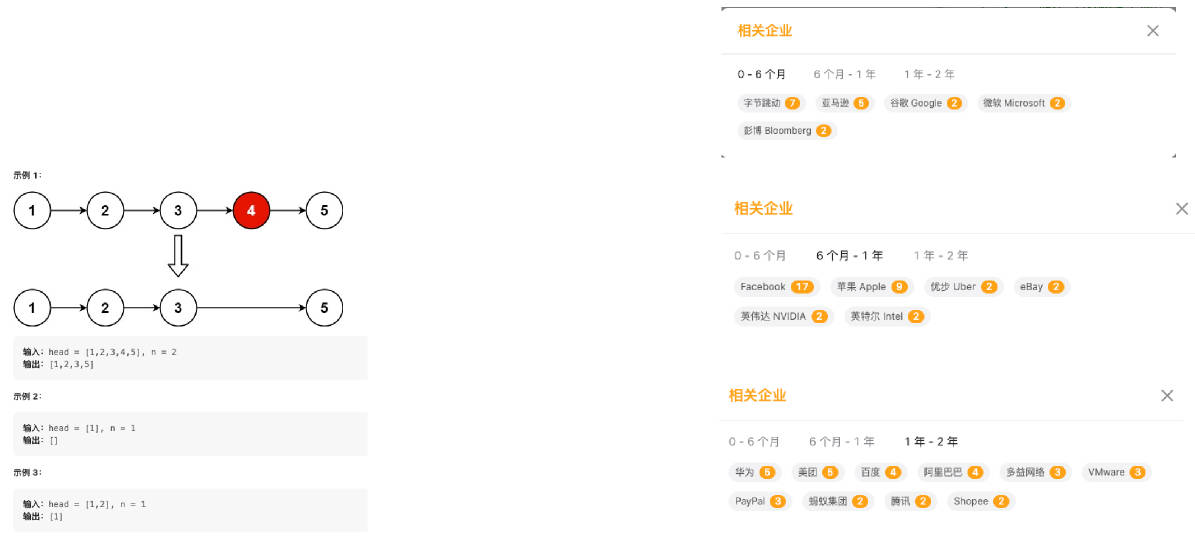
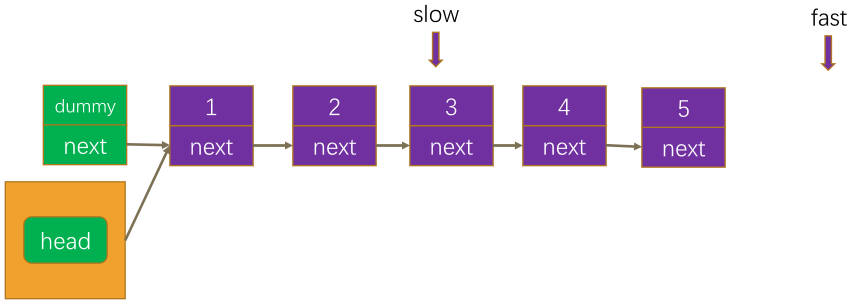
19.删除链表的倒数第 N 个结点（字节、谷歌等）

19.删除链表的倒数第 N 个结点

• https://leetcode.cn/problems/remove-nth-node-from-end-of-list/description/ 题目：
• 给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

删除链表的倒数第 N 个结点 – 代码实现

可以使用双指针来解决这个问题。

• 首先让快指针先移动 n 步，然后让慢指针和快指针一起移动，直到快指针到达链表末尾。

此时慢指针所指的节点就是要删除的节点的前一个节点，可以将其指向下下个节点，从而删除倒数第 n 个节点。

其中 dummy 节点是为了方便处理边界情况而添加的。

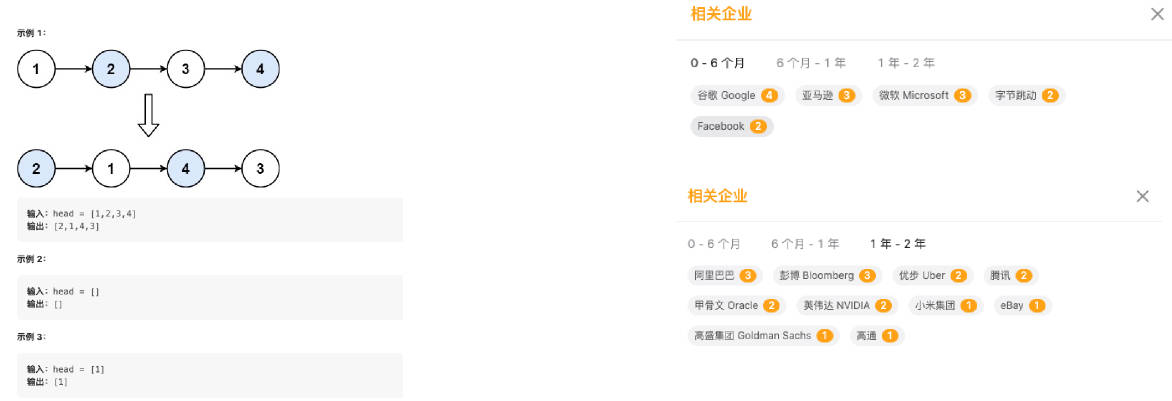
24.两两交换链表中的节点（谷歌、亚马逊、微软等）

24.两两交换链表中的节点

• https://leetcode.cn/problems/swap-nodes-in-pairs/description/

题目：

• 给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

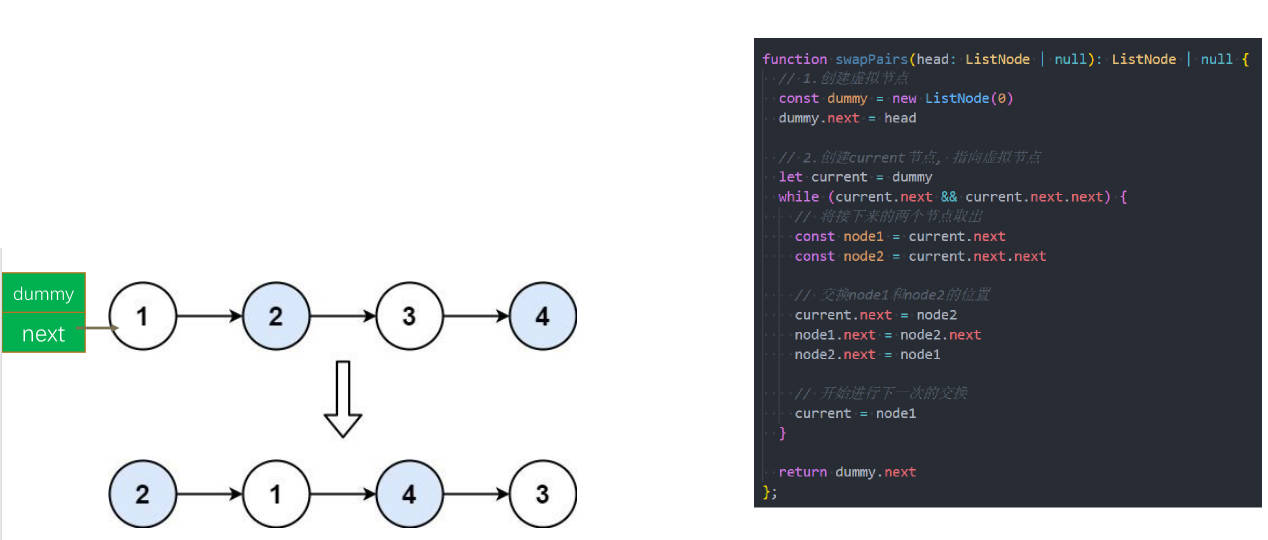
24.两两交换链表中的节点 – 代码实现

实现思路：

• 首先添加一个 dummy 节点；
• 创建一个 p 节点，默认指向虚拟节点（这里因为有虚拟节点，所以可以直接调用next）；
• 使用一个指针 p 依次指向每组相邻的节点，然后交换这两个节点的位置，直到遍历完整个链表。

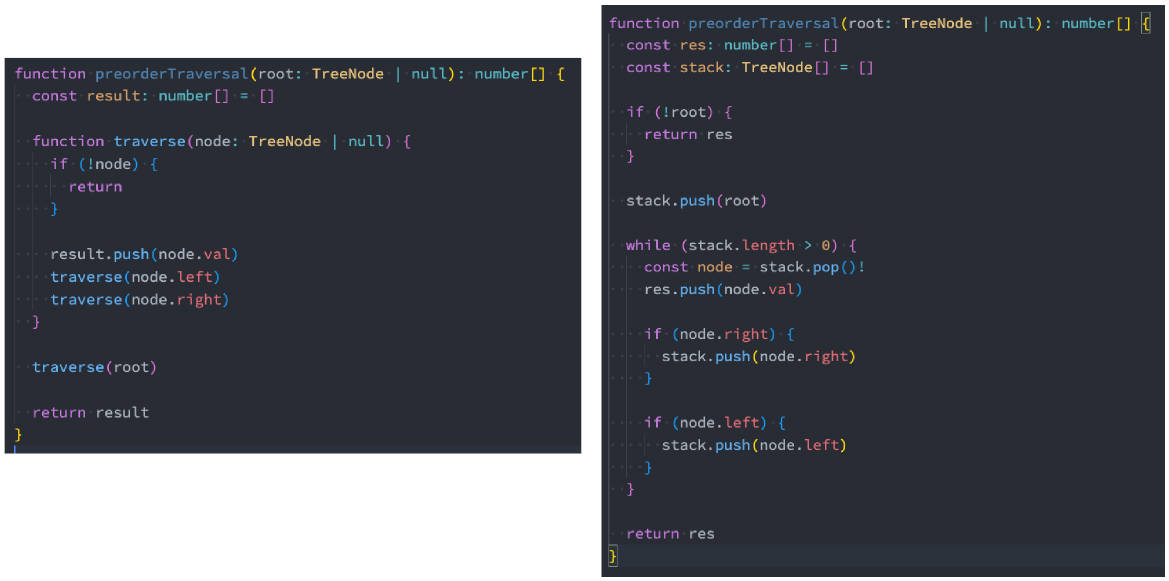
144. 二叉树的前序遍历（谷歌、微软、苹果等）

144.二叉树的前序遍历

• https://leetcode.cn/problems/binary-tree-preorder-traversal/

144. 二叉树的前序遍历（课下完成）

94.二叉树的中序遍历（亚马逊、谷歌、阿里等）

94.二叉树的中序遍历

• https://leetcode.cn/problems/binary-tree-inorder-traversal/

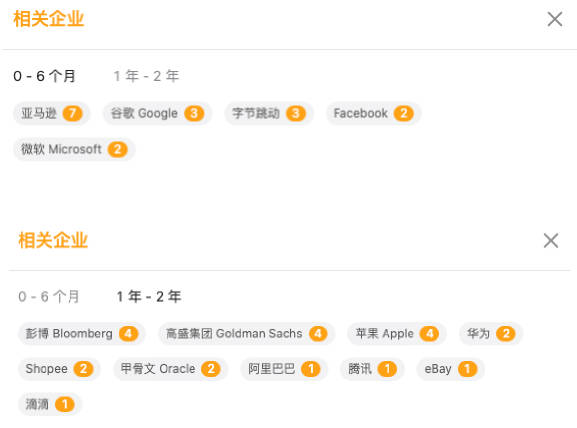
94.二叉树的中序遍历（课下完成）

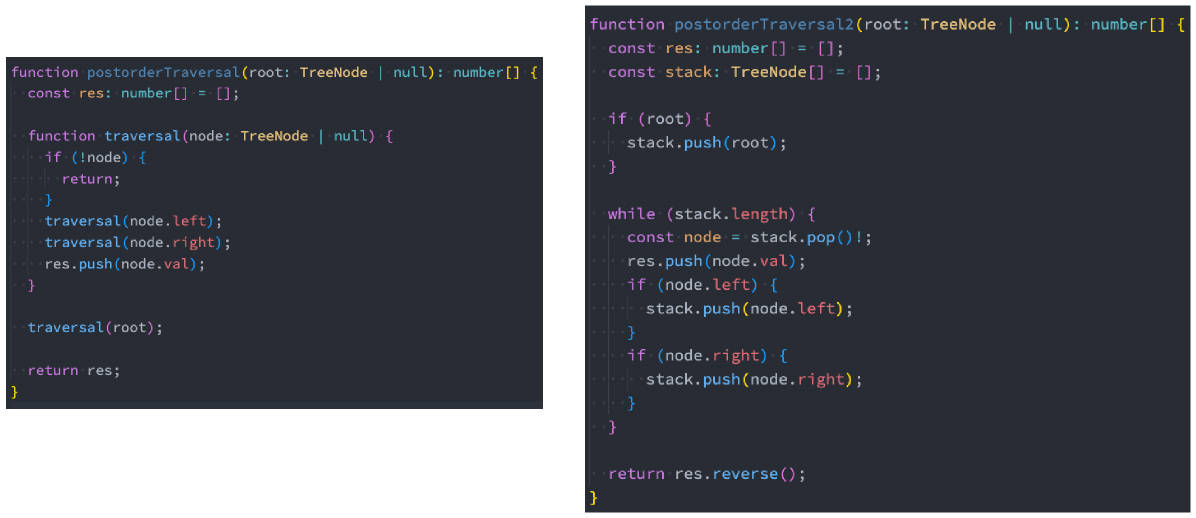
145.二叉树的后序遍历（字节、腾讯、苹果等）

145.二叉树的后序遍历

• https://leetcode.cn/problems/binary-tree-postorder-traversal/

145.二叉树的后序遍历（课下完成）

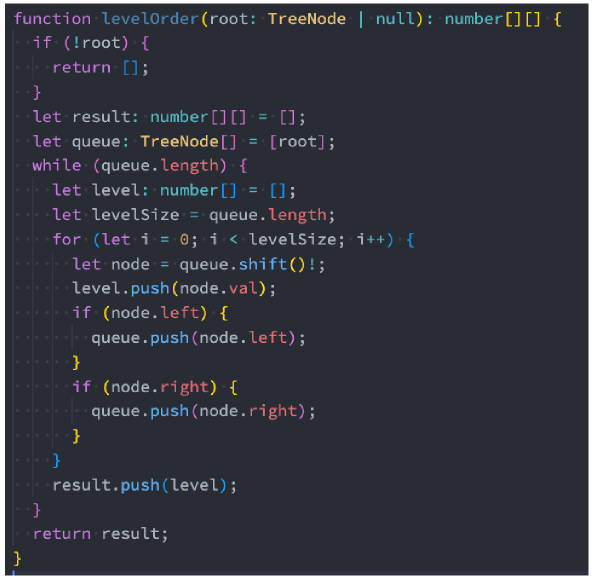
102.二叉树的层序遍历（字节、亚马逊、阿里等）

102.二叉树的层序遍历

• https://leetcode.cn/problems/binary-tree-level-order-traversal/description/

102.二叉树的层序遍历（课下完成）

226.翻转二叉树（亚马逊、微软、腾讯等）

226.翻转二叉树（Max Howell去Google面试没有写出来的题目）

• https://leetcode.cn/problems/invert-binary-tree/description/

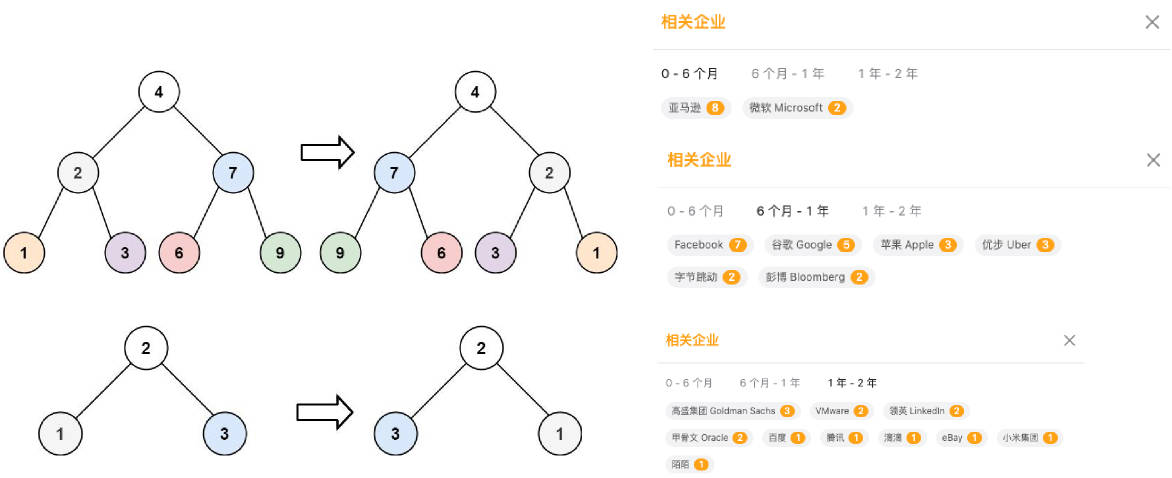
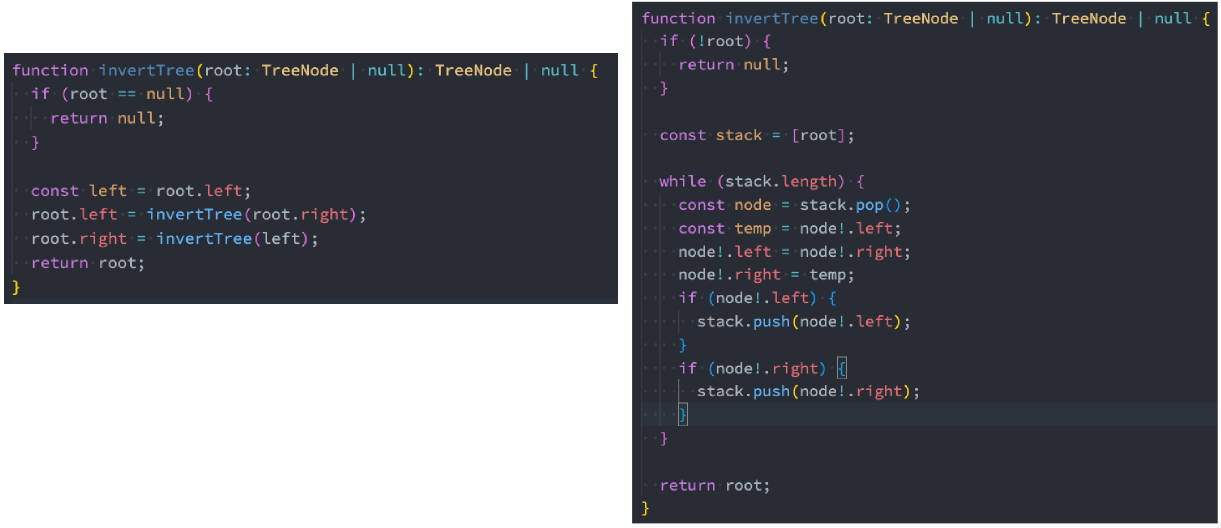
226.翻转二叉树

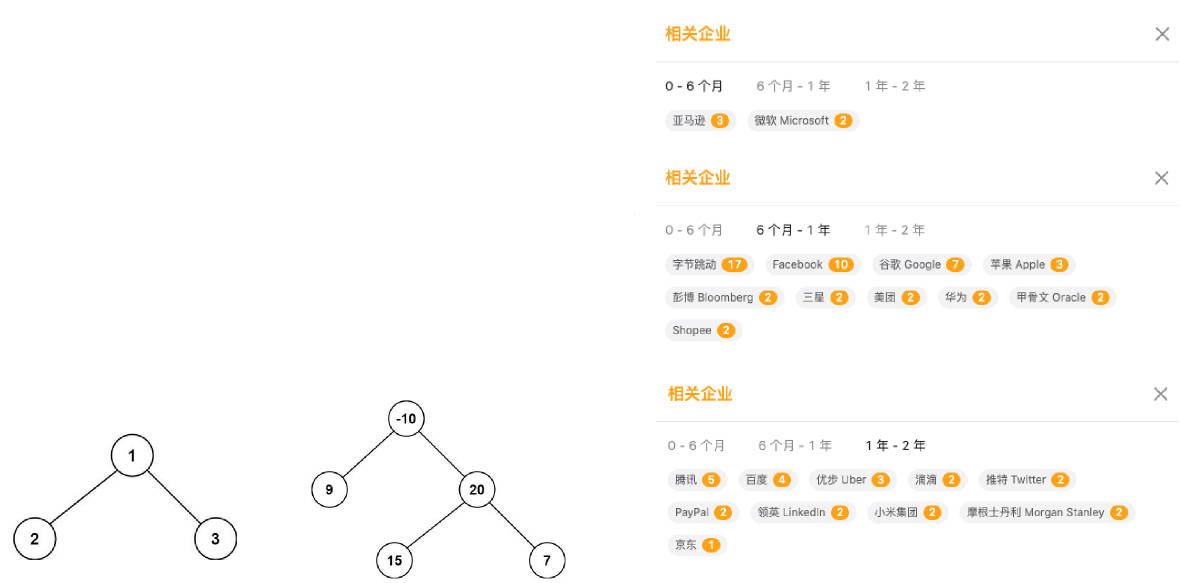
124.二叉树中的最大路径和（亚马逊、微软、腾讯等）

124.二叉树中的最大路径和

• https://leetcode.cn/problems/binary-tree-maximum-path-sum/description/ 题目：
• 路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root，返回其 最大路径和。

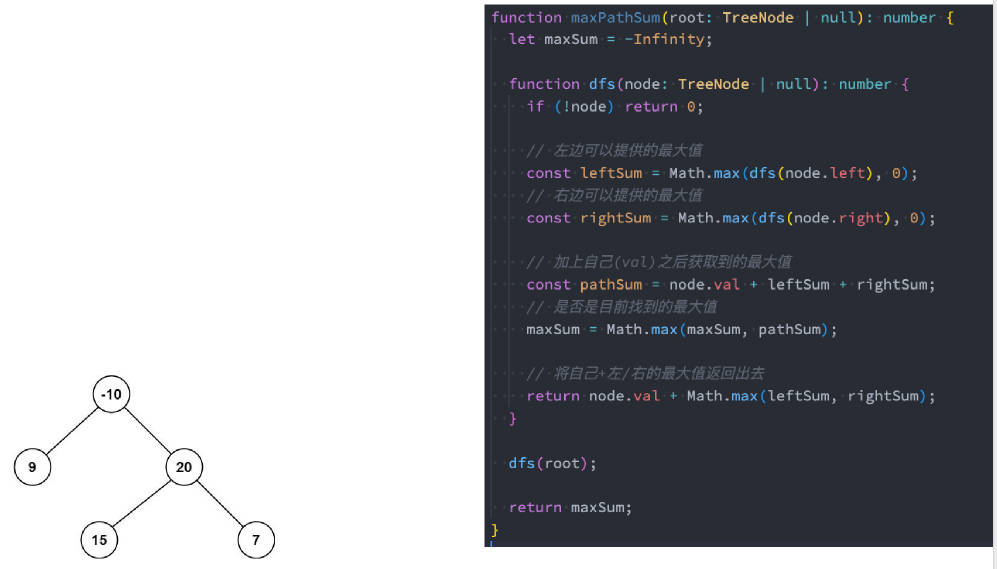
124.二叉树中的最大路径和

这道题目可以使用深度优先搜索（DFS）来解决。

• 我们可以从根节点开始递归，遍历二叉树中的所有节点。
• 对于每个节点，我们需要计算经过该节点的最大路径和。
  • 在计算经过该节点的最大路径和时，我们需要考虑到左子树和右子树是否能够贡献最大路径和。
  • 如果左子树的最大路径和大于 0，那么我们就将其加入到经过该节点的最大路径和中；
  • 如果右子树的最大路径和大于0，那么我们就将其加入到经过该节点的最大路径和中。

最后，我们将经过该节点的最大路径和与已经计算出的最大路径和进行比较，取两者中的较大值。

62.不同路径（亚马逊、谷歌、字节、腾讯等）

62.不同路径

• https://leetcode.cn/problems/unique-paths/description/

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start”）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

动态规划的实现思路

这个题目和跳楼梯其实是一类题目。 设 dp[i][j] 表示从起点到网格的(i, j)点的不同路径数。 对于每个格子，由于机器人只能从上面或左边到达该格子，因此有以下两种情况：

• 从上面的格子到达该格子，即 dp[i][j] = dp[i-1][j]；
• 从左边的格子到达该格子，即 dp[i][j] = dp[i][j-1]。
  • 因此，到达网格的 (i, j) 点的不同路径数就等于到达上面格子的路径数加上到达左边格子的路径数。
• 动态转移方程为：dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始状态：对于边界情况，起点的路径数为1，即 dp[0][0] = 1。

计算最终状态：dp[m-1][n-1]

不同路径的组合数学（课下扩展）

我们可以使用组合数学的方法，通过计算总共需要向下和向右走的步数，从而计算不同的路径数目。

假设总共需要向下走 n 步，向右走 m 步，则路径的总长度为 n + m，其中需要选择 n 个位置向下走，因此路径的总数目为 C(n + m, n)。

剑指 Offer 47.礼物的最大价值（字节、谷歌等）

剑指 Offer 47.礼物的最大价值

题目：

• https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof/description/

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

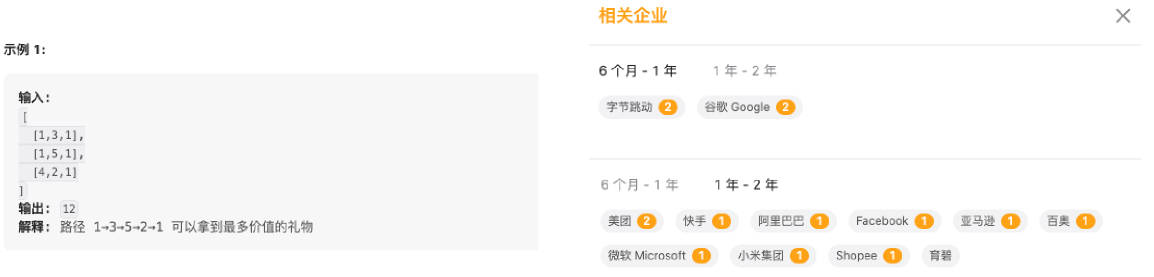
剑指 Offer 47.礼物的最大价值

300.最长递增子序列（亚马逊、谷歌、字节、华为等）

300.最长递增子序列（Longest Increasing Subsequence，简称LIS）

• https://leetcode.cn/problems/longest-increasing-subsequence/description/

题目：

• 给你一个整数数组nums，找到其中最长严格递增子序列的长度。
• 子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。

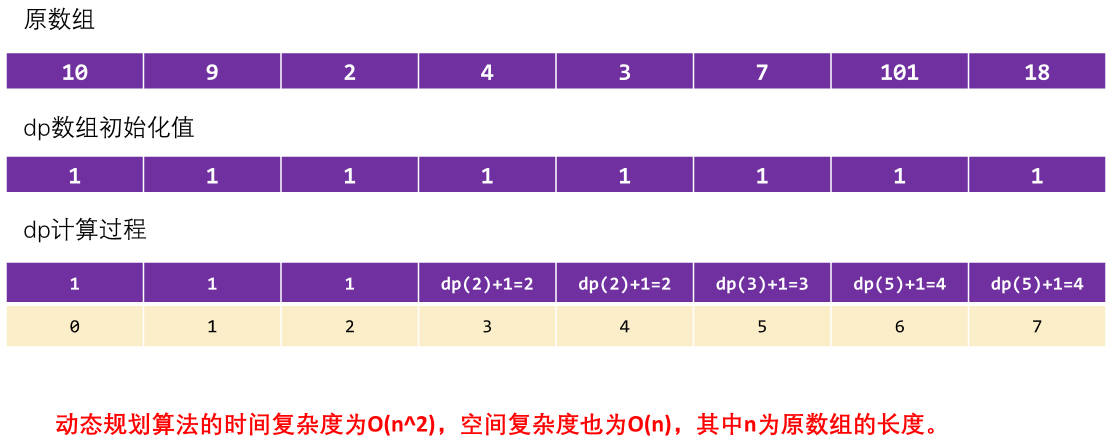
300.最长递增子序列–动态规划

这道题目可以使用动态规划来解决。 定义状态：设dp[i]表示以第i个元素结尾的最长上升子序列的长度。 状态转移方程：

• 对于每个i，我们需要找到在[0, i-1]范围内比nums[i]小的元素，以这些元素结尾的最长上升子序列中最长的那个子序列的长度。
• 然后将其加1即可得到以nums[i]结尾的最长上升子序列的长度。
• 状态转移方程为：dp[i] = max(dp[j]) + 1，其中j < i且nums[j] < nums[i]。 初始状态：对于每个i，dp[i]的初始值为1，因为每个元素本身也可以作为一个长度为1的上升子序列。 最终计算结果：最长上升子序列的长度即为dp数组中的最大值。

动态规划的计算过程

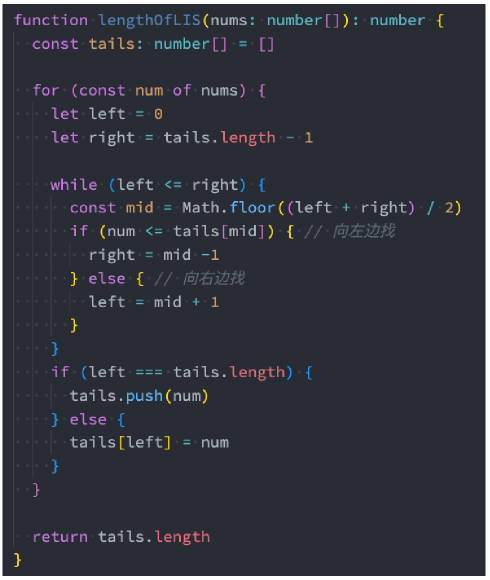
贪心+二分查找的思考过程

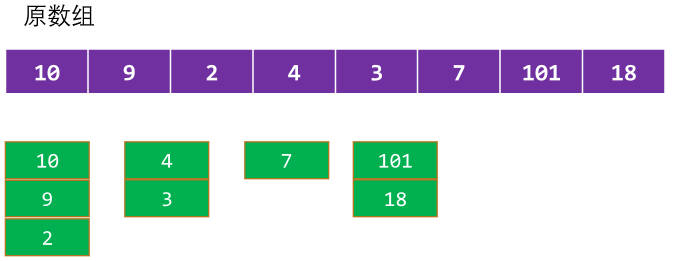
维护一个数组tails，用于记录扫描到的元素应该存放的位置。 扫描原数组中的每个元素num，在tails数组中找是否有比自己更大的值。

• 如果有，那么找到对应位置，并且让num作为该位置的最小值；
• 如果没有，那么直接放到tails数组的尾部； tails数组的长度，就是最长递增子序列的长度；

为什么这么神奇刚好是数组的长度呢？（了解）

情况一：如果是逆序的时候，一定会一直在一个上面加加加

情况二：一旦出现了比前面的最小值的值大的，那么就一定会增加一个新的数列，说明在上升的过程

情况三：如果之后出现一个比前面数列小的，那么就需要重新计算序列

贪心算法+二分查找的时间复杂度为O(nlogn)，空间复杂度为O(n)

贪心+二分查找的代码实现