平衡二叉树（AVL 树 – 红黑树）

平衡树（Balanced Tree）

平衡树（Balanced Tree）是一种特殊的二叉搜索树：

• 其目的是通过一些特殊的技巧来维护树的高度平衡；
• 从而保证树的搜索、插入、删除等操作的时间复杂度都较低；

为什么需要平衡树呢？

• 如果一棵树退化成链状结构，那么搜索、插入、删除等操作的时间复杂度就会达到最坏情况，即 O(n)，因此不能满足要求。
• 平衡树通过不断调整树的结构，使得树的高度尽量平衡，从而保证搜索、插入、删除等操作的时间复杂度都较低，通常为 O(logn)。
• 因此，如果我们需要高效地处理大量的数据，那么平衡树就显得非常重要了。

平衡树的应用非常广泛，如索引、内存管理、图形学等领域均有广泛使用。

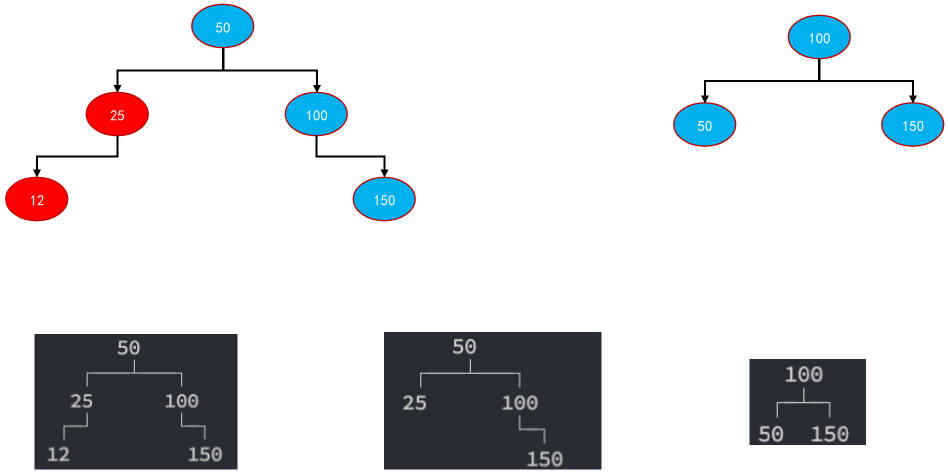
比如我们连续的插入 1、2、3、4、5、6 的数字，那么前面的二叉搜索树最终形成的结构如下

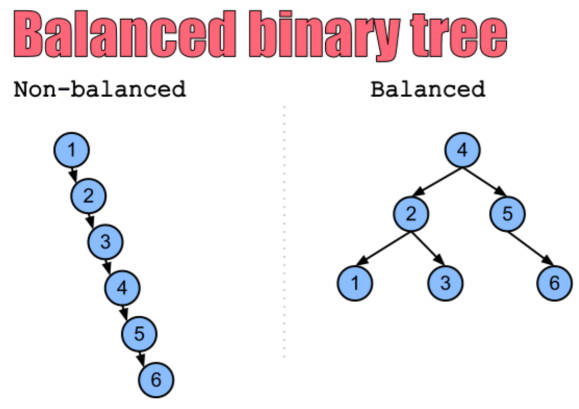
事实上不只是添加会导致树的不平衡，删除元素也可能会导致树的不平衡。

如何让树可以更加平衡呢？

方式一：限制插入、删除的节点（比如在树特性的状态下，不允许插入或者删除某些节点，不现实）

方式二：在随机插入或者删除元素后，通过某种方式观察树是否平衡，如果不平衡通过特定的方式（比如旋转），让树保持平衡。

常见的平衡二叉搜索树

常见的平衡二叉搜索树有哪些呢？

• AVL 树：这是一种最早的平衡二叉搜索树，在 1962 年由 G.M. Adelson-Velsky 和 E.M. Landis 发明。
• 红黑树：这是一种比较流行的平衡二叉搜索树，由 R. Bayer 在 1972 年发明。
• Splay 树：这是一种动态平衡二叉搜索树，通过旋转操作对树进行平衡。
• Treap：这是一种随机化的平衡二叉搜索树，是二叉搜索树和堆的结合。
• B-树：这是一种适用于磁盘或其他外存存储设备的多路平衡查找树。

这些平衡二叉搜索树都用于保证搜索树的平衡，从而在插入、删除、查找操作时保证了较低的时间复杂度。

红黑树和 AVL 树是应用最广泛的平衡二叉搜索树：

• 红黑树：红黑树被广泛应用于实现诸如操作系统内核、数据库、编译器等软件中的数据结构，其原因在于它在插入、删除、查找操作时都具有较低的时间复杂度。
• AVL 树：AVL 树被用于实现各种需要高效查询的数据结构，如计算机图形学、数学计算和计算机科学研究中的一些特定算法。

AVL 树

AVL 树（Adelson-Velsky and Landis Tree）是由 G.M. Adelson-Velsky 和 E.M. Landis 在 1962 年发明的

• 它是一种自（Self）平衡二叉搜索树。
• 它是二叉搜索树的一个变体，在保证二叉搜索树性质的同时，通过旋转操作保证树的平衡。

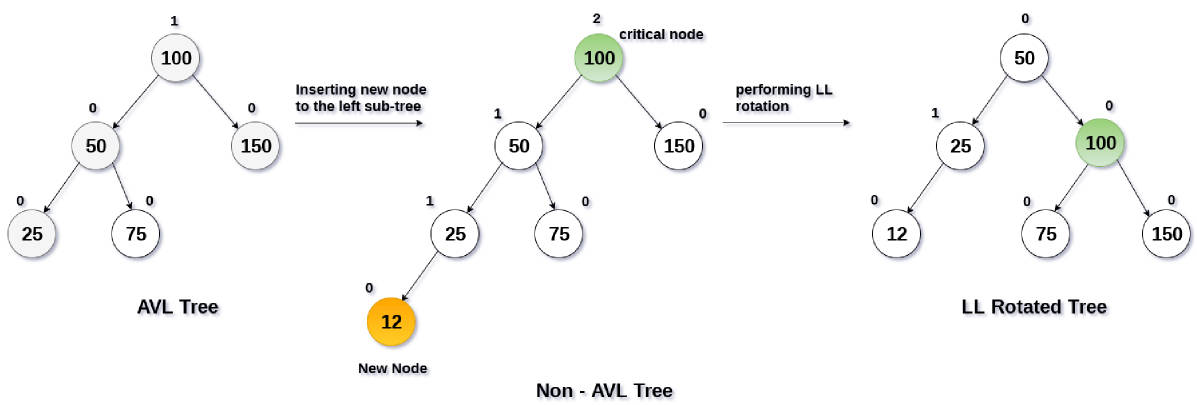
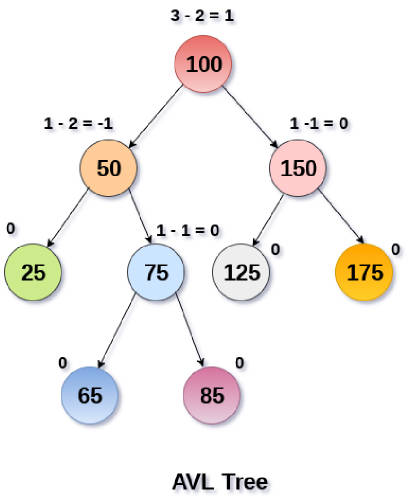
在 AVL 树中，每个节点都有一个权值，该权值代表了以该节点为根节点的子树的高度差。

• 在 AVL 树中，任意节点的权值只有 1 或-1 或 0，因此 AVL 树也被称为高度平衡树。
• 对于每个节点，它的左子树和右子树的高度差不超过 1。
• 这使得 AVL 树具有比普通的二叉搜索树更高的查询效率。
• 当插入或删除节点时，AVL 树可以通过旋转操作来重新平衡树，从而保证其平衡性。

AVL 树的插入和删除操作与普通的二叉搜索树类似，但是在插入或者删除之后，需要继续保持树的平衡。

• AVL 树需要通过旋转操作来维护平衡。
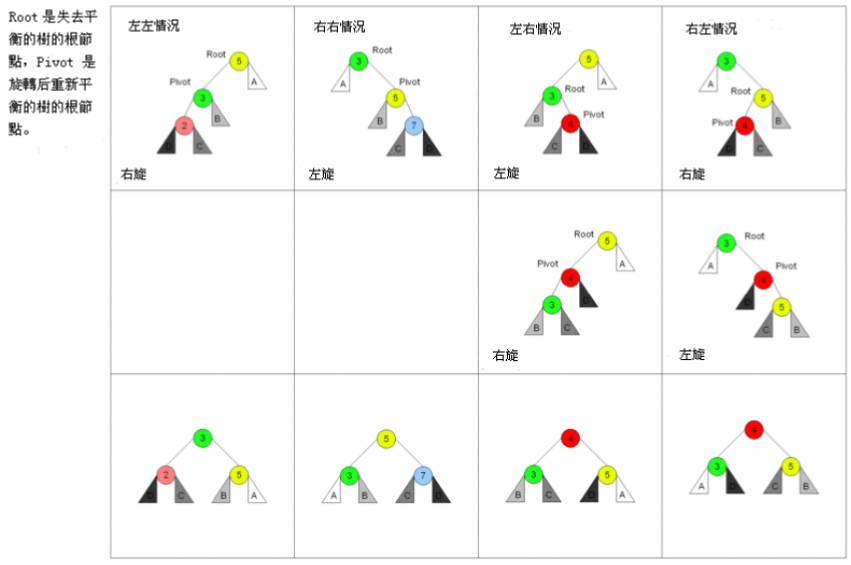
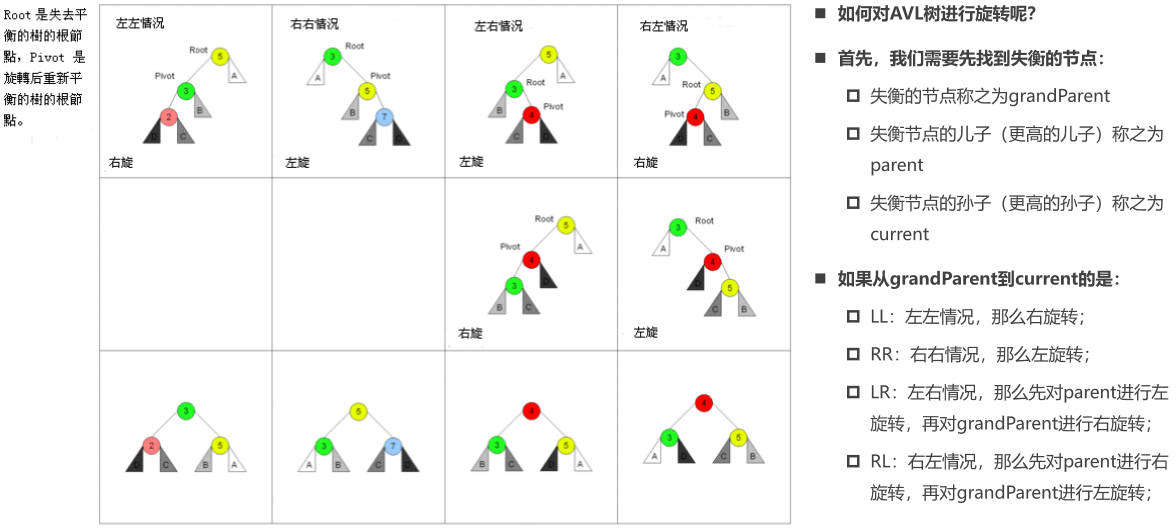
• 有四种情况旋转操作：左左情况、右右情况、左右情况和右左情况双旋。
• 具体使用哪一种旋转，要根据不同的情况来进行区分和判断。

由于 AVL 树具有自平衡性，因此其最坏情况下的时间复杂度仅 O(log n)。

AVL 树的旋转情况

AVL 树结构的封装过程

手写实现 AVL 树本身的过程是相当的复杂的，所以对于它的学习路线我进行了专门的设计。我们如何学习呢？

• 步骤一：学习 AVL 树节点的封装；
• 步骤二：学习 AVL 树的旋转情况下如何编写代码；
• 步骤三：写出不同情况下进行的不同旋转操作；
• 步骤四：写出插入操作后，树的再平衡操作；
• 步骤五：写出删除操作后，树的再平衡操作； 我们可以通过分治的思想，一步步实现上面的功能，再将功能组合在一起就完成了 AVL 树的编写过程。

AVLTreeNode – 节点的封装

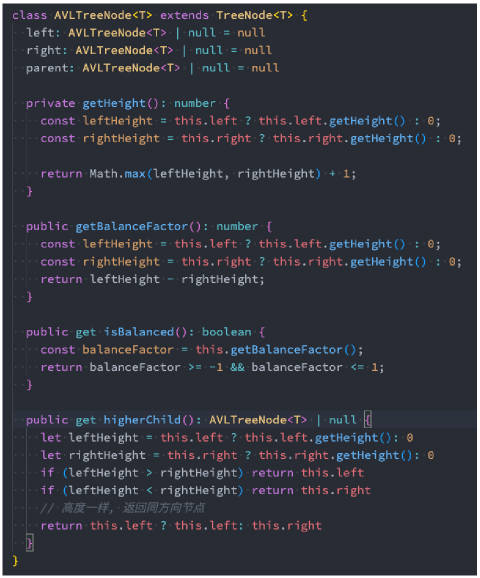
AVL 树的旋转 – 右旋转

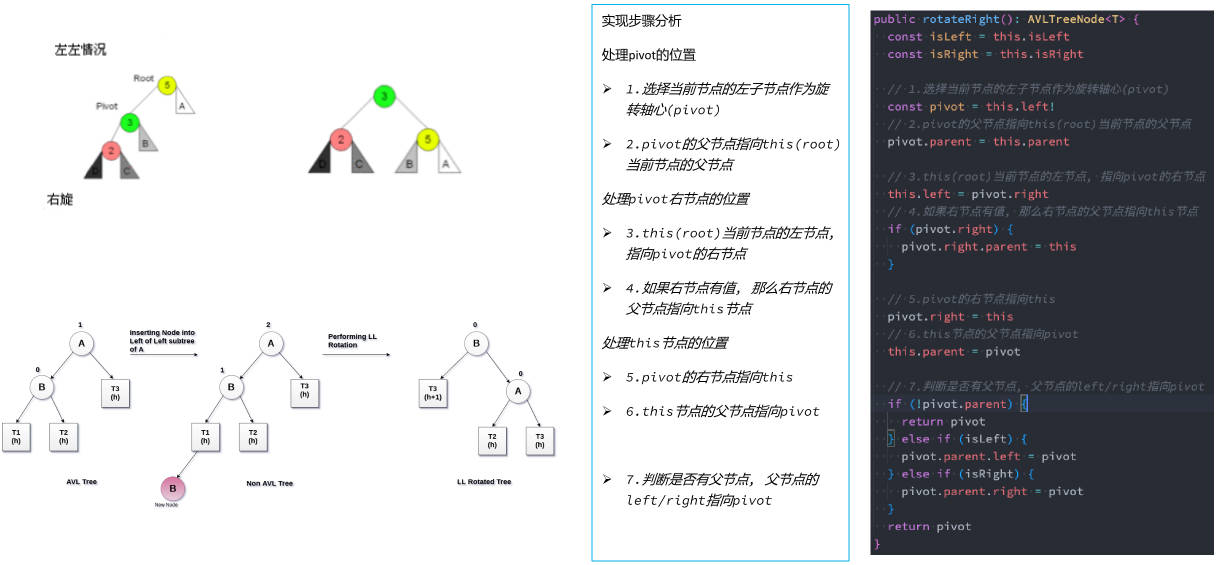
AVL 树的旋转 – 左旋转

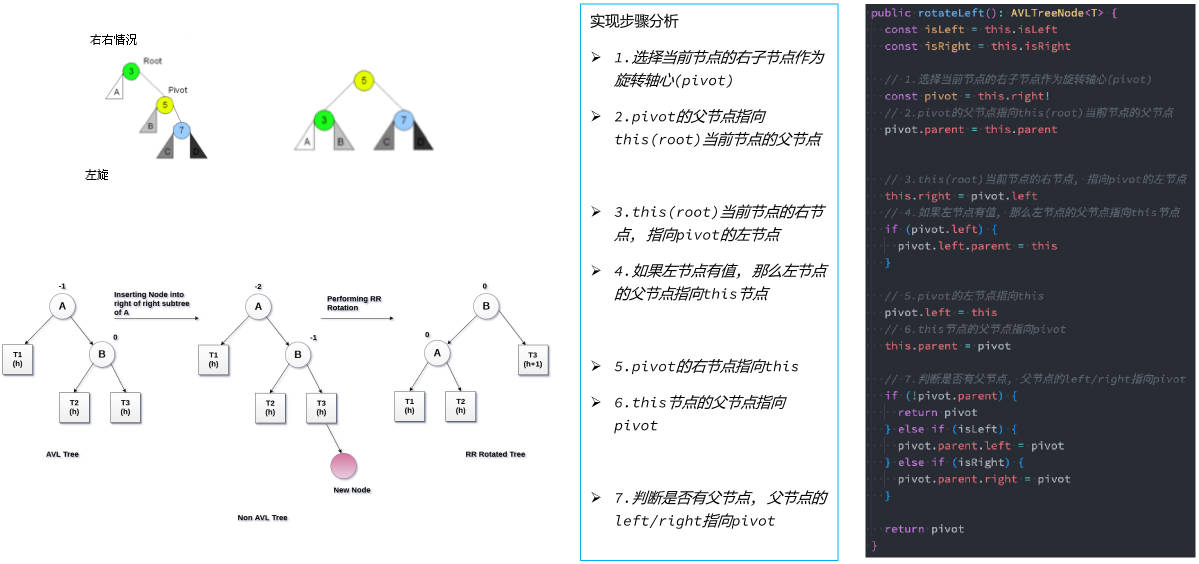
旋转的四种情况 - 分析

旋转的四种情况 - 代码实现

LL 的案例演示

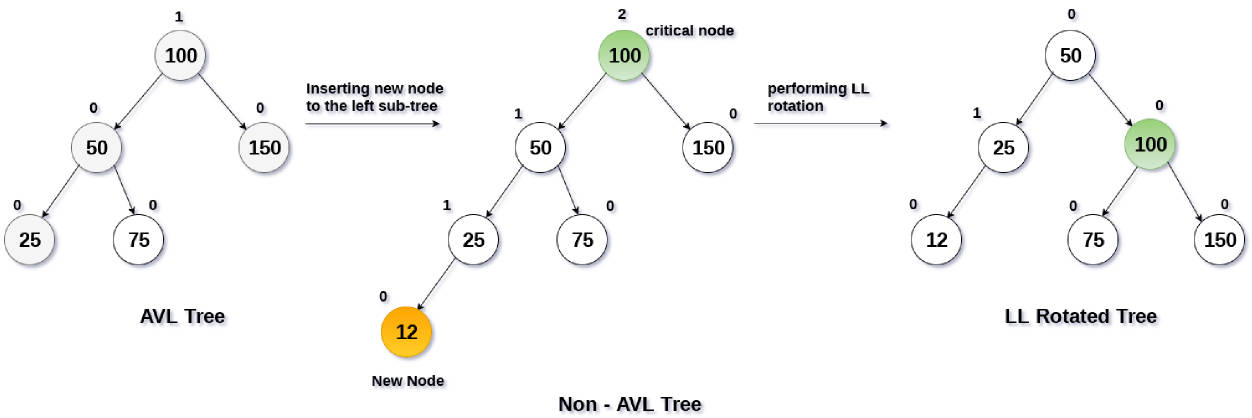
插入的案例演示

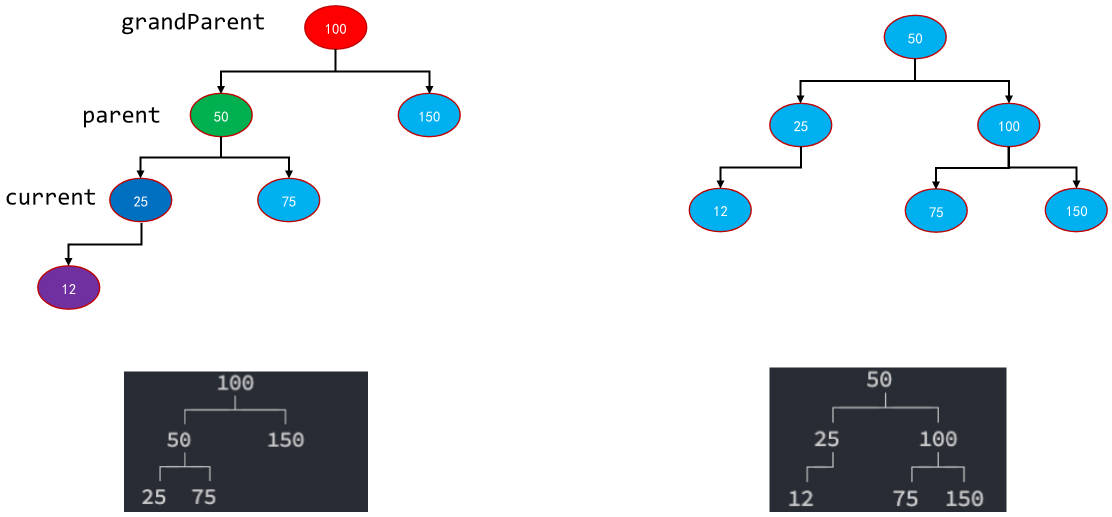
insert 的调整和再平衡

我们可以继续使用之前的插入操作，在插入完成后去检查树的平衡：

细节一 – Node 节点的类型

这里有一个小细节 - BSTree 插入的节点类型 TreeNode

我们可以封装一个模板方法，让子类来进行重写即可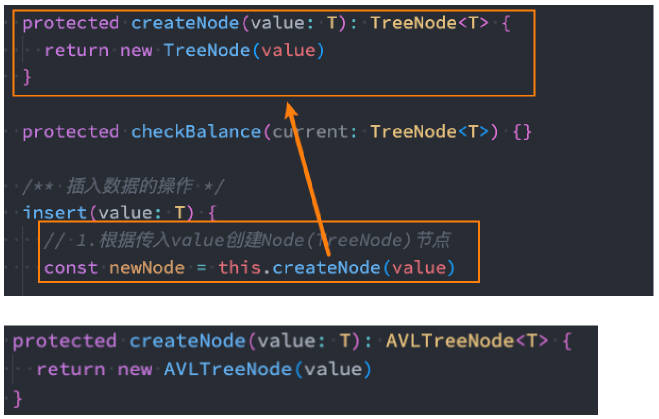

细节二 – Node 节点需要保存父节点

因为之后我们需要从当前节点中寻找 parent 节点，所以最好让每一个节点都保存一份 parent 节点（之前代码是不需要的）

随机插入数据的案例演示

我们可以随机一些数字，插入到 AVLTree 中来查看树是否平衡：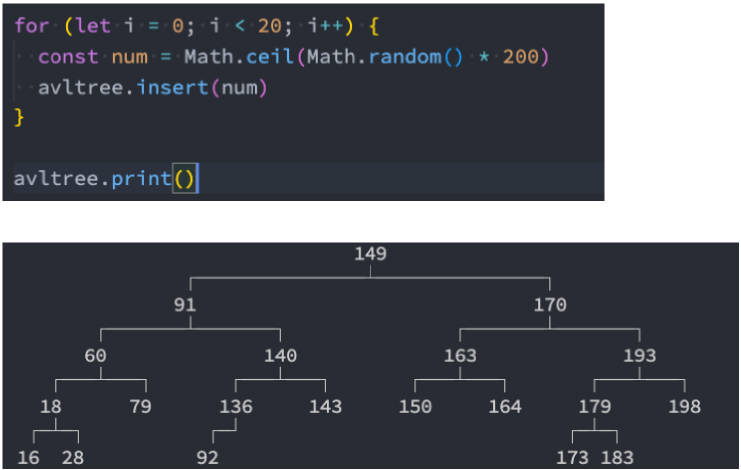

删除的案例演示

remove 的调整和再平衡

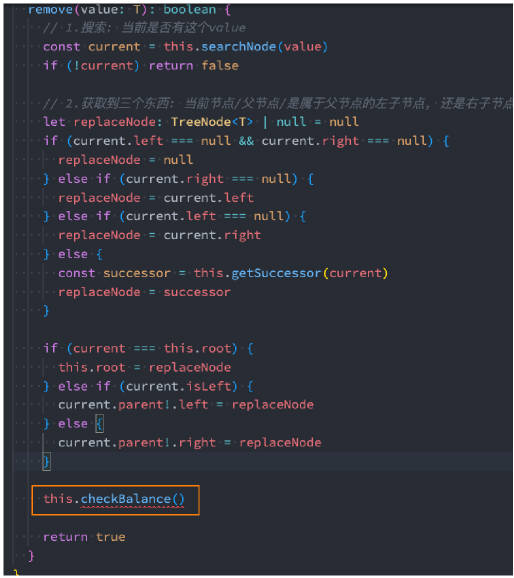
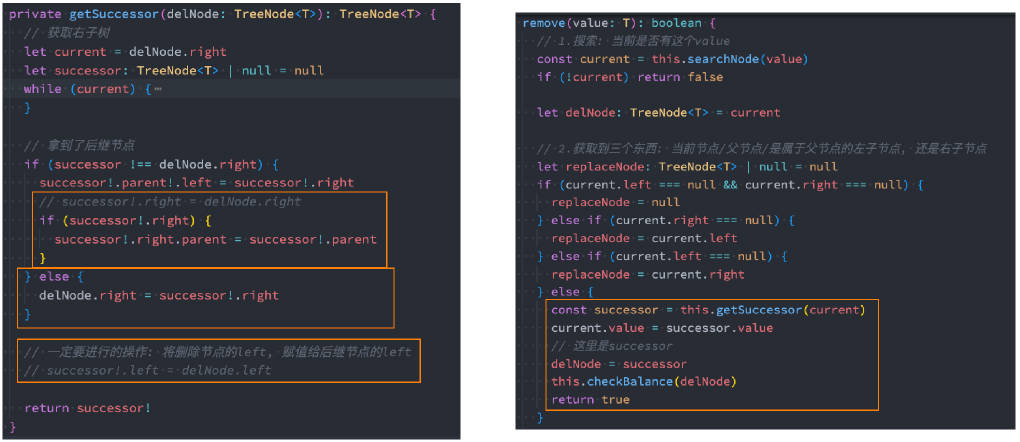
问题 – checkBalance 传入谁？

思考： checkBalance 传入谁？

• 很明显应该是删除的节点；
• 但是如果有两个子节点的情况，我们需要找的是前期和后继，最终是将前驱和后继位置的节点删除掉的；
• 寻找的应该是从 AVL 树中被移除位置的节点；

情况一：删除节点本身是叶子节点

• 传入 current 节点即可，并且需要根据 current 节点的 parent 去寻找失衡节点；

情况二：删除节点只有一个子节点

• 传入 current 节点即可，并且需要根据 current 节点的 parent 去寻找失衡节点；

情况三：删除节点有两个子节点：

• 找到后继节点 successor 原来的位置，并且需要根据 successor 节点去寻找失衡节点；

这里的关键点是两个：

• 关键点一：必须要找到检测位置的节点；
• 关键点二：检测位置的节点必须有父节点；

关键点一 – 寻找 delNode 节点

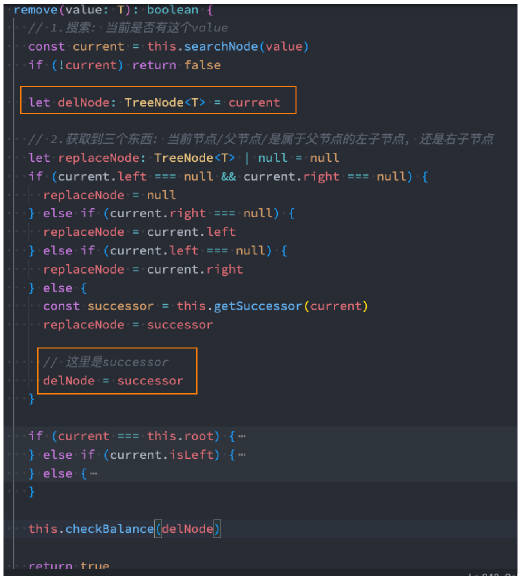
关键点二 – delNode 节点的父节点

情况一和情况二：

• delNode 节点有正确的父节点，但是后面的替换节点会失去正确的父节点；

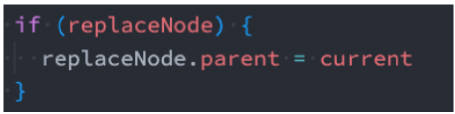
情况三：

• 如果需要找后继节点，那么父节点的操作会比较复杂；
• 我们可以利用我之前提到的第二种方案，来减少一些父节点的设置操作；

随机插入和删除测试

我们可以随机一些数字，插入，再删除，AVLTree 中来查看树是否平衡：

rebalance 的优化

目前我们 rebalance 的操作是哪些节点会执行呢？

• 插入节点的所有父节点（一直向上查找父节点）；
• 删除节点的所有父节点（一直向上查找父节点）；

但是 是否需要每次插入、删除都需要将所有的父节点都 rebalance 操作呢？

• 这个取决于在插入一个节点后后，是否改变了祖父节点的高度；
• 这个取决于在删除一个节点后后，是否改变了祖父节点的高度；

我们得出结论：

• 插入节点，再平衡rebalance后不需要继续后续节点的再平衡 rebalance ；
• 删除节点，再平衡rebalance后需要继续后续节点的再平衡 rebalance；

如何优化代码呢？

邂逅 红黑树

首先，红黑树是数据结构中很难的一个知识点，难到什么程度呢?

• 基本你跟别人聊数据结构的时候, 他不会和你聊红黑树, 因为它是数据结构中一个难点中的难点.
• 数据结构的学习本来就比较难了, 红黑树是又将难度上升一个档次的知识点.

面试的时候经常出现这个场景:

• 面试官: 你知道红黑树吗?
• 面试者: 知道啊。
• 面试官: 知道原理吗?
• 面试者: 不知道啊。
• 面试官: 那你让‘不’过来面试我们公司吧，你先回去等通知吧。

哪些面试会出现红黑树呢?

• 在面试时基本不会让手写红黑树（即使是面试 Google、Apple 这样的公司，也很少会出现）。
• 通常是这样问题的（比如腾讯的一次面试题）：为什么已经有平衡二叉树（比如 AVL 树）了，还需要红黑树呢？

红黑树的介绍

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构。

• 它在 1972 年由鲁道夫·贝尔发明，被称为“对称二叉 B 树”，它现代的名字源于 Leo J. Guibas 和罗伯特·塞奇威克于1978 年写的一篇论文。

红黑树, 除了符合二叉搜索树的基本规则外, 还添加了一下特性:

• 1.节点是红色或黑色。

• 2.根节点是黑色。

• 3.每个叶子节点都是黑色的空节点（NIL 节点，空节点）。

  ✓ 第三条性质要求每个叶节点（空节点）是黑色的

  ✓ 这是因为在红黑树中，黑色节点的数量表示从根节点到该节点的黑色节点数量。

• 4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

  ✓ 第四条性质保证了红色节点的颜色不会影响树的平衡，同时保证了红色节点的出现不会导致连续的红色节点。

• 5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

  ✓ 第五条性质是最重要的性质，保证了红黑树的平衡性。

这些规则会让人一头雾水

• 完成搞不懂规则叠加起来，怎么让一棵树平衡的。
• 但是它们还是被一些聪明的人发明出来了。

红黑树的图例

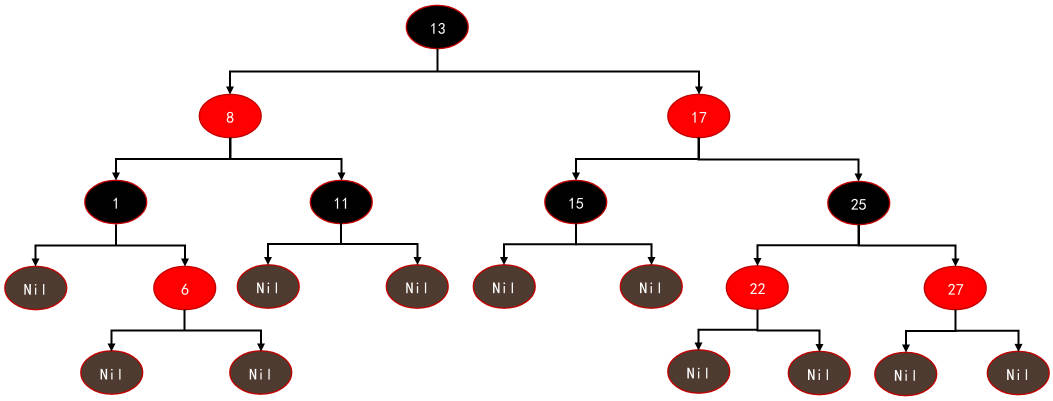
红黑树的相对平衡

前面的性质约束，确保了红黑树的关键特性:

• 从根到叶子的最长可能路径, 不会超过最短可能路径的两倍长。
• 结果就是这个树基本是平衡的.
• 虽然没有做到绝对的平衡，但是可以保证在最坏的情况下, 依然是高效的。

为什么可以做到 最长路径不超过最短路径的两倍 呢？

• 性质五决定了最短路径和最长路径必须有相同的黑色节点；

• 路径最短的情况：全部是黑色节点 n；

• 路径最长的情况：首尾解释黑色节点 n，中间全部是红色节点 n – 1；

  ✓ 性质二：根节点是黑节点；

  ✓ 性质三：叶子节点都是黑节点；

  ✓ 性质四：两个红色节点不能相连

• 最短路径为 n – 1（边的数量）；

• 最长路径为 (n + n – 1) - 1 = 2n – 2；

• 所以 最长路径 一定不超过 最短路径的 2 倍；

红黑树的代码实现

手写一个 TypeScript 红黑树的详细步骤：

• 定义红黑树的节点：定义一个带有键、值、颜色、左子节点、右子节点和父节点的类；
• 实现左旋操作：将一个节点向左旋转，保持红黑树的性质；
• 实现右旋操作：将一个节点向右旋转，保持红黑树的性质；
• 实现插入操作：在红黑树中插入一个新的节点，并保持红黑树的性质；
• 实现删除操作：从红黑树中删除一个节点，并保持红黑树的性质；
• 实现修复红黑树性质：在插入或删除操作后，通过旋转和变色来修复红黑树的性质；
• 其他方法较为简单，可以自行实现；

具体代码参考我的 Markdown 笔记。

红黑树的性能分析

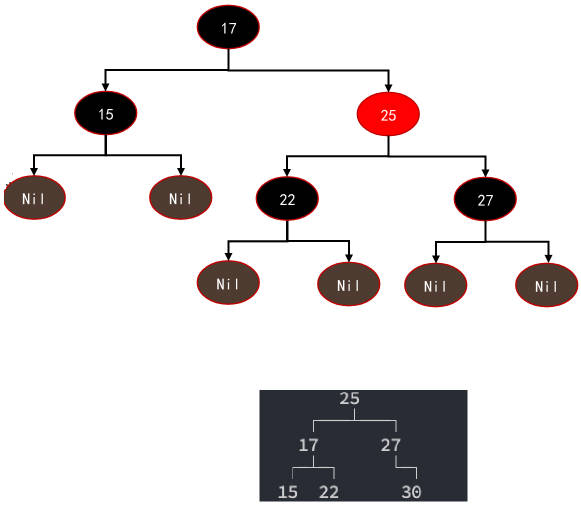
事实上，红黑树的性能在搜索上是不如 AVL 树的，为什么呢？

我们来看一下右边的红黑树：

• 首先，它符合是一颗红黑树吗？符合。

• 这个时候我们插入 节点 30，会被插入到哪里呢？

  ✓ 27 的右边，并且节点 30 是红色节点时，依然符合红黑树的性质。

• 也就是对于红黑树来说，它不需要进行任何操作；

那么 AVL 树会怎么样呢？

• 如果是 AVL 树必然要对 17、25、27 节点进行右旋转；
• 事实上右旋转是一系列的操作；

但是红黑树的高度比 AVL 树要高：

• 所以如果同样是搜索 30，那么红黑树需要搜索 4 次，AVL 树搜索 3 次；
• 所以红黑树相当于牺牲了一点点的搜索性能，来提高了插入和删除的性能；

AVL树和红黑树的选择

AVL树和红黑树的性能对比：

• AVL树是一种平衡度更高的二叉搜索树，所以在搜索效率上会更高；
• 但是AVL树为了维护这种平衡性，在插入和删除操作时，通常会进行更多的旋转操作，所以效率相对红黑树较低；
• 红黑树在平衡度上相较于AVL树没有那么严格，所以搜索效率上会低一些；
• 但是红黑树在插入和删除操作时，通常需要更少的旋转操作，所以效率相对AVL树较高；
• 它们的搜索、添加、删除时间复杂度都是O(logn)，但是细节上会有一些差异；

开发中如何进行选择呢？

• 选择AVL树还是红黑树，取决于具体的应用需求。
• 如果需要保证每个节点的高度尽可能地平衡，可以选择AVL树。
• 如果需要保证删除操作的效率，可以选择红黑树。

在早期的时候，很多场景会选择AVL树，目前选择红黑树的越来越多（AVL树依然是一种重要的平衡树）。

• 比如操作系统内核中的内存管理；
• 比如Java的TreeMap、TreeSet底层的源码；